Hckyplayer8
Full Member
- Joined
- Jun 9, 2019
- Messages
- 269
I browsed my book but I feel like I didn't really see any examples that fit the problem above.
Is there anything special about computing the integral of three functions as opposed to two?
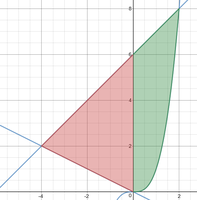
I plotted the functions and found their intersections at [-4,2],[0,0], and [2,8].
Is the next step just finding the definite integral bounded by x=-4, x=2 of all three functions?