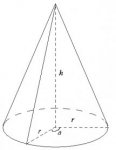
Height of the cone h and base radius r lengths ratio is equal to 4:3. From the cone was cut part, as shown in figure (a=1200).
How many times the cut part of the total surface area is less than the total surface area of a cone?
________
Hello,
I need help to solve this problem.
So, \(\displaystyle \frac{h}{r}=\frac{4}{3}\)
The total surfase area of the cone is: SA = πr(r + l).
How get formula of the cut part?
