You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
CRYPT multiplication 2
- Thread starter Saumyojit
- Start date
How did you get that? What did you do with my second hint?I have got only one lead that is E= 5 or 6 .
Nothing else.
e∗e=e+10α
when e is multiplied with e, it gives e +10x .
E cannot be zero so when 6*6 is multiplied we get 36 or 5*5= 25
please try to give more hint
You got 60% of what I wanted you to get out of that hint.
[MATH]e * e = e + 10\alpha \implies e = 0, \ e = 1, \ e = 5, \text { or } e = 6.[/MATH]
You missed one possibility, namely that e might be 1. But no harm was done because.
If e equals 0, the n * e = e, which differs from i. So e is not 0. If e equals 1, then n * e = n, which differs from i. So e is not equal to 1.
So, yes, e must be 5 or 6. Good job.
But there is more to get here. We can also determine that n does not equal 0 or 1. Do you see why?
Similarly, p does not equal 0 or 1. And obviously neither s nor h = 0.
Moreover, if e does equal 5, i must equal zero, n must be an even digit, p must be an odd digit, and beta (the carry digit from e * n) must exceed 0 but not exceed 4. Do you see why?
Consequently, I’d explore the e = 5 possibility first because it seems to be the more restrictive one.
[MATH]e * e = e + 10\alpha \implies e = 0, \ e = 1, \ e = 5, \text { or } e = 6.[/MATH]
You missed one possibility, namely that e might be 1. But no harm was done because.
If e equals 0, the n * e = e, which differs from i. So e is not 0. If e equals 1, then n * e = n, which differs from i. So e is not equal to 1.
So, yes, e must be 5 or 6. Good job.
But there is more to get here. We can also determine that n does not equal 0 or 1. Do you see why?
Similarly, p does not equal 0 or 1. And obviously neither s nor h = 0.
Moreover, if e does equal 5, i must equal zero, n must be an even digit, p must be an odd digit, and beta (the carry digit from e * n) must exceed 0 but not exceed 4. Do you see why?
Consequently, I’d explore the e = 5 possibility first because it seems to be the more restrictive one.
yes.if e does equal 5, i must equal zero, n must be an even digit, p must be an odd digit, and beta (the carry digit from e * n) must exceed 0 but not exceed 4. Do you see why?
Then, how to proceed
D
Deleted member 4993
Guest
What did you try?yes.
Then, how to proceed
You need to understand that I have not worked these out before I give a response. I have suggested some general methods, but the two primary ones are (1) be systematic and (2) make assumptions and try to prove them wrong.
The first thing I would do is write down what I know about the obvious unknowns and the number of equations.
There are 8 obvious unknown digits, and t, p, s, and h are greater than 0 by the rules of the puzzle.
There are 15 equations. There are 14 unknown carry digits.
Now there are other things you can determine by the rules.
You figured out correctly that e = 5 or 6. I pointed out that n must be greater than 1 as must p.
From there I suggested that you assume temporarily that e = 5. In that case, i = 0, n is even, and p is odd.
[MATH]\text {Moreover } 125 \le 100t + 10h + 5 \le 985 \implies 625 \le 5(100t + 10h + 5) \le 4925.[/MATH]
Therefore p = 1 or 3 and t > 1. Why? What next?
The first thing I would do is write down what I know about the obvious unknowns and the number of equations.
There are 8 obvious unknown digits, and t, p, s, and h are greater than 0 by the rules of the puzzle.
There are 15 equations. There are 14 unknown carry digits.
Now there are other things you can determine by the rules.
You figured out correctly that e = 5 or 6. I pointed out that n must be greater than 1 as must p.
From there I suggested that you assume temporarily that e = 5. In that case, i = 0, n is even, and p is odd.
[MATH]\text {Moreover } 125 \le 100t + 10h + 5 \le 985 \implies 625 \le 5(100t + 10h + 5) \le 4925.[/MATH]
Therefore p = 1 or 3 and t > 1. Why? What next?
how did you derived thisMoreover 125≤100t+10h+5≤985⟹625≤5(100t+10h+5)≤4925.Moreover 125≤100t+10h+5≤985⟹625≤5(100t+10h+5)≤4925.\displaystyle \text {Moreover } 125 \le 100t + 10h + 5 \le 985 \implies 625 \le 5(100t + 10h + 5) \le 4925.
why'd u writeen this
I don't understand
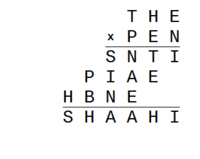
THE is supposed to be a three digit number and t is a digit so
[MATH]1 \le t \le 9[/MATH], right.
By the rules, each letter stands for a distinct digit. We are assuming for right now that e = 5, which means i = 0 so h is not zero. Therefore the letter represented by THE cannot be less than 125, right? And it cannot be more than 985, right?
We have E times THE. But we are assuming e = 5. Therefore e times THE must be at least 625 and at most 4925.
But that product is a four digit number with an initial digit of p. So p cannot exceed 4. And we have previously determined that p > 1 and that p is odd if e = 5. Thus if e = 5, i = 0, p = 3, and n is even.
[MATH]1 \le t \le 9[/MATH], right.
By the rules, each letter stands for a distinct digit. We are assuming for right now that e = 5, which means i = 0 so h is not zero. Therefore the letter represented by THE cannot be less than 125, right? And it cannot be more than 985, right?
We have E times THE. But we are assuming e = 5. Therefore e times THE must be at least 625 and at most 4925.
But that product is a four digit number with an initial digit of p. So p cannot exceed 4. And we have previously determined that p > 1 and that p is odd if e = 5. Thus if e = 5, i = 0, p = 3, and n is even.
We have previously determined 1 or 3.p = 1 or 3
How do you say p>1?
Do you agree that if p = 1 then p * e = e with no carry because e is a decimal digit?
So, p = 1 and p(10h + 0) = 10n entails that 10h = 10n or h = n, which is contrary to the rules of the puzzle. So p is not 1.
I do apologize. My explanation of that was abysmal. But you also do need to create equations.
So, p = 1 and p(10h + 0) = 10n entails that 10h = 10n or h = n, which is contrary to the rules of the puzzle. So p is not 1.
I do apologize. My explanation of that was abysmal. But you also do need to create equations.
D
Deleted member 4993
Guest
Shape of the spoon is very clear though......Do you agree that if p = 1 then p * e = e with no carry because e is a decimal digit?
So, p = 1 and p(10h + 0) = 10n entails that 10h = 10n or h = n, which is contrary to the rules of the puzzle. So p is not 1.
I do apologize. My explanation of that was abysmal. But you also do need to create equations.
e=5, i=0, n is even , p=3, 1≤t≤9 .Do you agree that if p = 1 then p * e = e with no carry because e is a decimal digit?
So, p = 1 and p(10h + 0) = 10n entails that 10h = 10n or h = n, which is contrary to the rules of the puzzle. So p is not 1.
I do apologize. My explanation of that was abysmal. But you also do need to create equations.
Now what to do? please tell the full logic
@Saumyojit
You seem to be under the illusion that I have solved this puzzle. I have not. I have shown you a method. You need to apply it.
A warning. We do not know for sure that e = 5. That is an assumption.
You need to write things down. On the supposition that e = 5, i = 0, p = 3, and n is even, make equations and then be systematic about identifying and then excluding possibilities.
[MATH](350 + 2k)(100t + 10h + 5) = 35000t + 3500h + 1750 + 200k + 20kh + 10k[/MATH]
What can you tell me about H?
You seem to be under the illusion that I have solved this puzzle. I have not. I have shown you a method. You need to apply it.
A warning. We do not know for sure that e = 5. That is an assumption.
You need to write things down. On the supposition that e = 5, i = 0, p = 3, and n is even, make equations and then be systematic about identifying and then excluding possibilities.
[MATH](350 + 2k)(100t + 10h + 5) = 35000t + 3500h + 1750 + 200k + 20kh + 10k[/MATH]
What can you tell me about H?
how did you derived this(350+2k)(100t+10h+5)=35000t+3500h+1750+200k+20kh+10k(350+2k)(100t+10h+5)=35000t+3500h+1750+200k+20kh+10k\displaystyle (350 + 2k)(100t + 10h + 5) = 35000t + 3500h + 1750 + 200k + 20kh + 10k
For goodness sake, PEN is supposed to be a three digit number and the letters represent digits so it equalshow did you derived this
[MATH]100p + 10e + n[/MATH]
But we are operating under the assumption that p = 3, e = 5, and n is an even number
[MATH]\therefore n = 2k \text { and } 100p + 10e + n = 300 + 50 + 2k = 350 + 2k.[/MATH]
So what number does THE represent?
What is the product of those two numbers?
Do we have another representation of that product?
What can you derive about h?
THE * PEN=10^5 *S+H*10^4+ A* 10^3+ A*10^2 +H*10+IDo we have another representation of that product?
THE * PEN= 35t * 10^3 + 35h *10^2 + 1750 +200 kt +20kh+ 10k
10^5 *S+H*10^4+ A* 10^3+ A*10^2 +H*10+I= 35t * 10^3 + 35h *10^2 + 1750 +200 kt +20kh+ 10k
NothingWhat can you derive about h?
We are on the right track as I have seen the value of E and p in the answer .
E=5 , p=3 . Good work in derving the value of p
Please others assist.
Please end this sum by today
Last edited:
okay the sum is done
THE * 5 = 30A5
H*5 +2= A Now i know that 5*T=30 where T=6 so no carry
so H=1 so A=7.
The way u derived p=3 is really commendable @JeffM
Yes This is actually true.
More conditions means that assumption has a higher chance of doing the work
THE * 5 = 30A5
H*5 +2= A Now i know that 5*T=30 where T=6 so no carry
so H=1 so A=7.
The way u derived p=3 is really commendable @JeffM
, I’d explore the e = 5 possibility first because it seems to be the more restrictive one.
Yes This is actually true.
More conditions means that assumption has a higher chance of doing the work
Last edited: