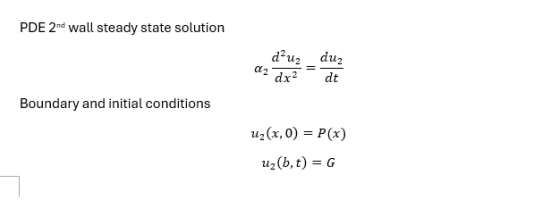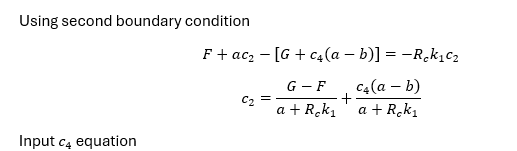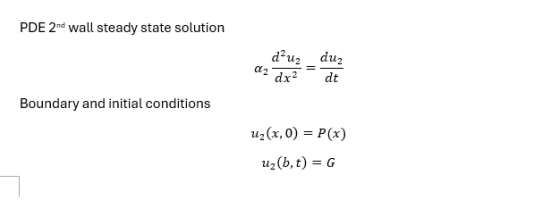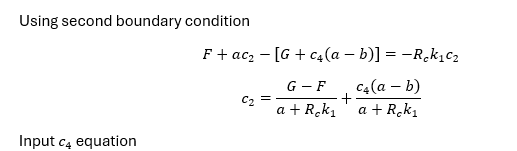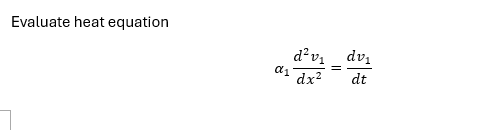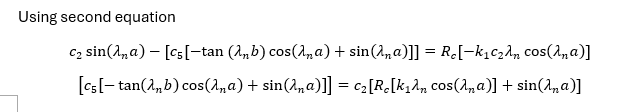You are right. I ignored the contact resistance to make your calculations easier. But if you want to include it and be tough, it is your call. In this case, the calculations will be very difficult even for the steady state solution. If you like challenges, this is a really good one of them.
View attachment 39502
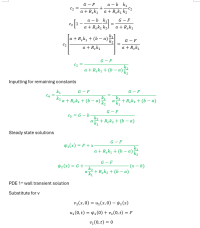
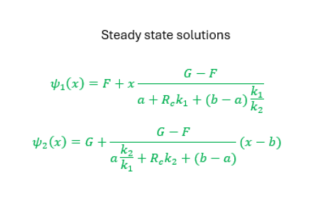
I checked your steady solutions. They are correct and also MATLAB confirms this as you said. That was one simple tough task!
Now when I read your transient solution, I think that you made a big mistake unintentionally
 \(\displaystyle \alpha_1\) and \(\displaystyle \alpha_2\) don't belong to the time solution \(\displaystyle T(t)\). Instead they belong the spatial solution \(\displaystyle X(x)\). I understand why you have made this mistake! Because you are used to do that when you solve a normal partial differential equation. But when we solve a system of two equations we want both time functions to decay in the same time. If you put \(\displaystyle \alpha_1\) and \(\displaystyle \alpha_2\) in the time equations, the time functions will decay in different times. This violates the whole system process.
\(\displaystyle \alpha_1\) and \(\displaystyle \alpha_2\) don't belong to the time solution \(\displaystyle T(t)\). Instead they belong the spatial solution \(\displaystyle X(x)\). I understand why you have made this mistake! Because you are used to do that when you solve a normal partial differential equation. But when we solve a system of two equations we want both time functions to decay in the same time. If you put \(\displaystyle \alpha_1\) and \(\displaystyle \alpha_2\) in the time equations, the time functions will decay in different times. This violates the whole system process.
I think that this might be the reason why your transient solution gives wrong results. When the spatial functions don't have \(\displaystyle \alpha_1\) and \(\displaystyle \alpha_2\), you get wrong eigenvalues \(\displaystyle \lambda_n\). My intuition tells me that was the error that let the system produced wrong data. Fix it and let me know if your problem is solved.