Determine the equation for the tangent line of the function that has the largest slope

prokrastinera said:
The function: f(x) = 6/x^2+3.

Had a hard time solving this. Can you solve it too with steps?
Click to expand...
Did you read posting guidlines? Where are you stuck? Did you try to draw the graph and a few tangent lines?
 
The first thing you would do is differentiate: \(\displaystyle f'(x)= (6x^(-2)+ 3)'= -12x^(-3)\). The tangent line to y= f(x) at \(\displaystyle x_0\) is \(\displaystyle y= (-12x_0^{-3})(x- x_0)+ 6x_0^2+ 3\). You say "has the largest slope". The slope if that gets arbitrarily large as x nears 0.

Did you mean \(\displaystyle f(x)= 6/(x^2+ 3)= 6(x^2+ 3)^{-1}\)? \(\displaystyle f'= -12x(x^2+ 3)^{-2}\). Where is that maximum?
 
HallsofIvy said:
The first thing you would do is differentiate: \(\displaystyle f'(x)= (6x^(-2)+ 3)'= -12x^(-3)\). The tangent line to y= f(x) at \(\displaystyle x_0\) is \(\displaystyle y= (-12x_0^{-3})(x- x_0)+ 6x_0^2+ 3\). You say "has the largest slope". The slope if that gets arbitrarily large as x nears 0.

Did you mean \(\displaystyle f(x)= 6/(x^2+ 3)= 6(x^2+ 3)^{-1}\)? \(\displaystyle f'= -12x(x^2+ 3)^{-2}\). Where is that maximum?
Click to expand...
Yes I mean 1590594441186.png
 
HallsofIvy said:
The first thing you would do is differentiate: \(\displaystyle f'(x)= (6x^(-2)+ 3)'= -12x^(-3)\). The tangent line to y= f(x) at \(\displaystyle x_0\) is \(\displaystyle y= (-12x_0^{-3})(x- x_0)+ 6x_0^2+ 3\). You say "has the largest slope". The slope if that gets arbitrarily large as x nears 0.

Did you mean \(\displaystyle f(x)= 6/(x^2+ 3)= 6(x^2+ 3)^{-1}\)? \(\displaystyle f'= -12x(x^2+ 3)^{-2}\). Where is that maximum?
Click to expand...
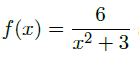
Could you write your answer on paper and post it? I really need to pass this exam... ?
 
Take the derivative. Now you have the derivative which is just a function. Now you want to know the max of this function. How do you find the max of a function???
 
You must log in or register to reply here.
Top