You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Dividing a quadrilateral: Can every quadrilateral be divided to 2 triangles?
- Thread starter shahar
- Start date
Can every quadrilateral be divided to 2 triangles?0
What is the definition of a quadrilateral - according to your textbook?
shahar
Full Member
- Joined
- Jul 19, 2018
- Messages
- 535
polygon of 4 sides.What is the definition of a quadrilateral - according to your textbook?
It is a riddle. It isn't written in textbook.
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
There aren't really only two examples. Either you can simply connect any two opposing points, or you can only connect one set of opposing points.Can every quadrilateral be divided to 2 triangles?
-Dan
The Highlander
Senior Member
- Joined
- Feb 18, 2022
- Messages
- 1,196
Yes.Can every quadrilateral be divided to 2 triangles?
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
This would be a far more interesting discussion if you would tell us your own thoughts. Did you have a reason to think the answer is yes? Did you have a reason to be unsure of your answer? Did you try a number of different quadrilaterals, including both convex and concave? All of that is worth talking about.Can every quadrilateral be divided to 2 triangles?
shahar
Full Member
- Joined
- Jul 19, 2018
- Messages
- 535
Yes the solutions is looking about convex polygon and concave polygon.
1. There is the article I was referred to:
Someone tell me that this article show why it is true.
2. My thoughts is using elimination to show all the cases one-by-one, to show all the possiblites that it true.
1. There is the article I was referred to:
Someone tell me that this article show why it is true.
2. My thoughts is using elimination to show all the cases one-by-one, to show all the possiblites that it true.
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
Are you saying that your question is based on a problem you found somewhere that mentions convex and concave? Please show us the problem!Yes the solutions is looking about convex polygon and concave polygon.
Or are you just saying that you recognize that convex and concave is relevant?
Why would you believe them? The article is about an entirely different problem (and far larger). I see no mention of triangles.1. There is the article I was referred to:
Someone tell me that this article show why it is true.
What are "all the cases"? There are an infinite number of quadrilaterals.2. My thoughts is using elimination to show all the cases one-by-one, to show all the possibilities that it true.
Do you mean, show first that any convex quadrilateral can be divided into two triangles in two ways, and then that any concave quadrilateral can be divided into two triangles in one way?
Please show your work. The interesting part of the proof, I think, will be to prove that all concave quadrilaterals are in a sense the same, so that one proof will handle that case.
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
I can't read the article.Yes the solutions is looking about convex polygon and concave polygon.
1. There is the article I was referred to:
Someone tell me that this article show why it is true.
2. My thoughts is using elimination to show all the cases one-by-one, to show all the possiblites that it true.
Just how "deep" of a proof are you looking for? Visually, there are really only two examples: one where you can connect opposite points without crossing the lines of the quadrilateral (the convex case), and one where you can't (the concave case.) But in both cases there is a way to connect at least one pair of opposite points.
What more of a proof are you looking for?
-Dan
shahar
Full Member
- Joined
- Jul 19, 2018
- Messages
- 535
I think about using the fact that the sum of the angles in triagnle is 180 degrees.
When we pass a line to the opposite vertex we divided the area to 2. The angles that created is external angle that influence on the other angles in the other triangle.
Because the quadriletral is a polygon that compose from 360 degrees there can't be any sum that greater from 360 degrees.
So, I think by showing that the figure is a polygon with 180 degrees can define as triangles.
By using the property that the have excatly 180 degrees, I prove that the figures that created is 2 triangles.
I think my proof is for convex quadriletral
When we pass a line to the opposite vertex we divided the area to 2. The angles that created is external angle that influence on the other angles in the other triangle.
Because the quadriletral is a polygon that compose from 360 degrees there can't be any sum that greater from 360 degrees.
So, I think by showing that the figure is a polygon with 180 degrees can define as triangles.
By using the property that the have excatly 180 degrees, I prove that the figures that created is 2 triangles.
I think my proof is for convex quadriletral
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
Please draw pictures of a convex quadrilateral and a concave quadrilateral, and think about whether your reasoning is true in every case (regardless of the starting vertex).I think about using the fact that the sum of the angles in triagnle is 180 degrees.
When we pass a line to the opposite vertex we divided the area to 2. The angles that created is external angle that influence on the other angles in the other triangle.
Because the quadriletral is a polygon that compose from 360 degrees there can't be any sum that greater from 360 degrees.
So, I think by showing that the figure is a polygon with 180 degrees can define as triangles.
By using the property that the have excatly 180 degrees, I prove that the figures that created is 2 triangles.
I think my proof is for convex quadriletral
The Highlander
Senior Member
- Joined
- Feb 18, 2022
- Messages
- 1,196
I don't understand how this has become so complicated! ?
Unless the original question was not framed correctly. ?
Regardless of whether it's concave or convex it is always possible to connect at least one pair of vertices of any quadrilateral to create two triangles!
As @topsquark has succinctly explained (twice!). ?
Should the original question have referred to any polygon instead of any quadrilateral? ?
Unless the original question was not framed correctly. ?
Regardless of whether it's concave or convex it is always possible to connect at least one pair of vertices of any quadrilateral to create two triangles!
As @topsquark has succinctly explained (twice!). ?
Should the original question have referred to any polygon instead of any quadrilateral? ?
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
If we just want a direct answer to the question itself (is it true?), it's already been said repeatedly that the answer is yes. Yes, that's a simple question.I don't understand how this has become so complicated!
I then opened it up to the bigger question, to make it interesting: How do we know it's true, and why did @shahar have to ask it? That makes it just a little more complicated, because now we are talking about how to think, not just what to think, and there are different ways to think. My suggestion is that just drawing two pictures may be enough; but more may be wanted, and even that hasn't been done yet.
shahar
Full Member
- Joined
- Jul 19, 2018
- Messages
- 535
The question in the file I get was truncated.lIf we just want a direct answer to the question itself (is it true?), it's already been said repeatedly that the answer is yes. Yes, that's a simple question.
I then opened it up to the bigger question, to make it interesting: How do we know it's true, and why did @shahar have to ask it? That makes it just a little more complicated, because now we are talking about how to think, not just what to think, and there are different ways to think. My suggestion is that just drawing two pictures may be enough; but more may be wanted, and even that hasn't been done yet.
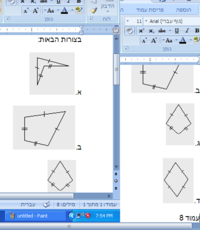
The original question:
Can every quadrilateral divided to 2 triangles
in the pictures below:
(list of pictures of quadrilaterals).
The underline text was truncate and appears in the next page.
Thanks you about trying to help me.
Good Day.
The next month is New (Hebrew) Year.
So, Happy New Year.
Shana Tuva (in Hebrew: Happy New Year).
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
So, are you satisfied with the answer? If there is more you are unsure of, you might show us the pictures (along with your own way of dividing each quadrilateral).
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
I assume you know how to divide each of these into two triangles?Here the file.
Happy New Year.
shahar
Full Member
- Joined
- Jul 19, 2018
- Messages
- 535
Yes.I assume you know how to divide each of these into two triangles?