logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
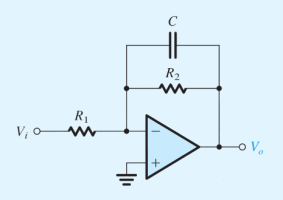
The figure shows a circuit that performs a low-pass STC function. Such a circuit is known as a first-order low-pass active filter. Derive the transfer function and show that the dc gain is \(\displaystyle \left(-\frac{R_2}{R_1}\right)\) and the \(\displaystyle 3\)-\(\displaystyle \text{dB}\) frequency \(\displaystyle \omega_{\tiny 0} = \frac{1}{CR_2}\). Design the circuit to obtain an input resistance of \(\displaystyle 10 \ \text{k}\Omega\), a dc gain of \(\displaystyle 40 \ \text{dB}\), and a \(\displaystyle 3\)-\(\displaystyle \text{dB}\) frequency of \(\displaystyle 1 \ \text{kHz}\). At what frequency does the magnitude of the transfer function reduce to unity?