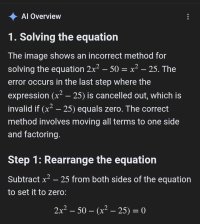
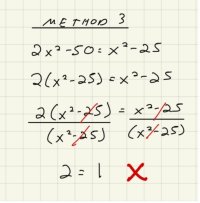Hi everyone, I have hit a conundrum with a problem (see screenshot below). I can't figure out why I'm getting 2 = 1 for Method 3. I'm trying a lot of different ways to manipulate equations/expressions and this one has stumped me. I know I'm not solving for x in Method 3, but I thought both sides should be equal since they both equal 0.


Last edited: