logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
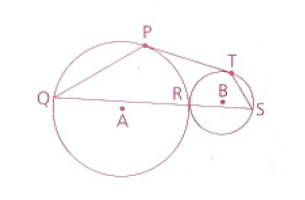
\(\displaystyle \bold{Given}\): \(\displaystyle \text{\large$\odot$}\text{A}\) is tangent to \(\displaystyle \text{\large$\odot$}\text{B}\) at \(\displaystyle \text{R}\). \(\displaystyle \overline{\text{PT}}\) is a common external tangent at \(\displaystyle \text{P}\) and \(\displaystyle \text{T}\). \(\displaystyle \angle\text{Q} = 43^{\circ}\). \(\displaystyle \bold{Find}\) \(\displaystyle \angle\text{S}\).