slice_of_god
New member
- Joined
- Nov 5, 2013
- Messages
- 6
it's a Equilateral triangle.
find the "X".
thank you.
find the "X".
thank you.
find the "X"
- Thread starter slice_of_god
- Start date
How is the x that you are supposed to find defined?it's a Equilateral triangle.
find the "X".
thank you.
What have you tried?
Is it possible that \(\displaystyle x\) is the side of the triangle?
Is it possible you know the law of cosines?
Show us your work! WE don't know what YOU know!
slice_of_god
New member
- Joined
- Nov 5, 2013
- Messages
- 6
yes i know the law of cosines.
the X is the side of triangle.
Bob Brown MSEE
Full Member
- Joined
- Oct 25, 2012
- Messages
- 598
6.77 on side
There are three triangles in which \(\displaystyle x^2\) can be found as functions of angles \(\displaystyle \alpha,\ \beta,\ \gamma\), using the Law of Cosines.
A fourth equation is
........\(\displaystyle \alpha+ \beta +\gamma = 2\pi \)
In principle, that is four (independent) equations in four unknowns, so a solution exists.
How to find the solution requires either trig, geometric construction, or lucky guesswork. Part of the trickiness may be how to construct a 3-4-5 triangle, in which you would recognize the angle between sides of 3 and 4 is is a right angle.
I started looking at it from the trig point of view.
Note that \(\displaystyle \alpha = 2\pi - (\beta+\gamma)\), from which
.........\(\displaystyle \cos\alpha = \cos(\beta + \gamma) = \cos\beta\cos\gamma - \sin\beta\sin\gamma\)
That leads to some complicated algebra, but might lead to an equation for \(\displaystyle x\) in closed form.
It is also true that
.........\(\displaystyle \sin\alpha = -\sin(\beta + \gamma) = -(\sin\beta\cos\gamma + \cos\beta\sin\gamma)\)
[I don't know if that is any help or not.]
Did you look up the geometric solution that Denis found?
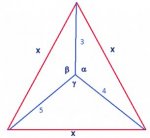
A hint from that solution is that \(\displaystyle \alpha = 90° + 60° = 150°\). If you can prove that somehow, then the problem is solved.Denis said:
These are only some musings - what have YOU tried?