Hello everyone,
Some colleagues and me have ran into a very specific problem and we are unable to get any further. Let me introduce the issue.
We construct different conversion curves for the purchasing behavior of a product by assigning the percentage of people that are willing to buy on each offered normalized price. We interpret this curves as probability density functions or pdf.
In the image below are some examples of the experimental results we are getting.
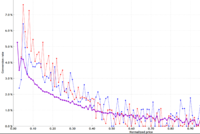
As you can see the lower the price the higher the conversion rate as one might expect. This curves follow an analytical expression ( generalized sigmoid ) that we can fit with good results.
The purple curve is the general conversion curve p(x) being x=normalized price. The blue and red curves are the conversion curves given some condition for example the city where the product is being purchased C.
So for the city a we have the blue curve p(x|C=a) and the red curve p(x|C=b) for the city b.
Then we could repeat the same exercise and construct the conversion curves given some other condition for example the day of the week which the product is being purchased D.
So in this case we can construct 7 different curves being p(x|D=mon), p(x|D=tue), p(x|D=wed), ..., p(x|D=sun)
Building these curves given one a single condition from real data is possible because our datasets are big enough, but if we want to find a curve combining two conditions simultaneously like city = a and day of the week = sunday we find ourselves lacking enough experimental data to build such curves, since with fewer datapoints the noise become unmanageable and we get gaps in the experimental curve where no data is found for some normalized prices.
The question would be that since we can compute experimentally the conversion curve for the city a p(x|C=a) and the curve for mondays p(x|D=mon) is there a way to combine these two experimental results and find analytically or numerically the conversion curve of the city a during mondays i.e. p(x|C=a, D=mon) given these two?
We have thought extensively about this and we couldn't find anything in the literature and we wonder if it is even possible.
Thank you for your time !
Some colleagues and me have ran into a very specific problem and we are unable to get any further. Let me introduce the issue.
We construct different conversion curves for the purchasing behavior of a product by assigning the percentage of people that are willing to buy on each offered normalized price. We interpret this curves as probability density functions or pdf.
In the image below are some examples of the experimental results we are getting.

As you can see the lower the price the higher the conversion rate as one might expect. This curves follow an analytical expression ( generalized sigmoid ) that we can fit with good results.
The purple curve is the general conversion curve p(x) being x=normalized price. The blue and red curves are the conversion curves given some condition for example the city where the product is being purchased C.
So for the city a we have the blue curve p(x|C=a) and the red curve p(x|C=b) for the city b.
Then we could repeat the same exercise and construct the conversion curves given some other condition for example the day of the week which the product is being purchased D.
So in this case we can construct 7 different curves being p(x|D=mon), p(x|D=tue), p(x|D=wed), ..., p(x|D=sun)
Building these curves given one a single condition from real data is possible because our datasets are big enough, but if we want to find a curve combining two conditions simultaneously like city = a and day of the week = sunday we find ourselves lacking enough experimental data to build such curves, since with fewer datapoints the noise become unmanageable and we get gaps in the experimental curve where no data is found for some normalized prices.
The question would be that since we can compute experimentally the conversion curve for the city a p(x|C=a) and the curve for mondays p(x|D=mon) is there a way to combine these two experimental results and find analytically or numerically the conversion curve of the city a during mondays i.e. p(x|C=a, D=mon) given these two?
We have thought extensively about this and we couldn't find anything in the literature and we wonder if it is even possible.
Thank you for your time !
Last edited:
