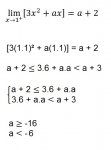You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Finding limit: if lim[x->1^+] (3x^2+ax) = a+2, find values of "a"
- Thread starter Farzin
- Start date
I'll be honest, I'm really struggling to follow any of the work you've shown. I can tell you, however, that both your solution and your daughter's solution are wrong. Whenever you want to know if an answer is correct or not, you can always plug the answer in to the original problem and see if it checks. Your daughter's solution is any value less than -16 for 'a'." So let's pick a = -20 as a nice round number to test.
\(\displaystyle \displaystyle \lim _{x\to 1+}\left(3x^2-20x \right) = 3(1)^2-20(1)=-17\) and \(\displaystyle a+2=-20+2=-18\)
Oops. That doesn't check out. That means your daughter's solution is wrong. Your solution says that -16 <= a < -6. Let's pick -10 as a nice round value in that interval.
\(\displaystyle \displaystyle \lim _{x\to 1+}\left(3x^2-10x \right) = 3(1)^2-10(1)=-7\) and \(\displaystyle a+2=-10+2=-8\)
Uh oh. That also doesn't check out. So, now that we've proven that neither your solution nor your daughter's solution is correct, let's set to finding what the correct answer actually is and why you went wrong. I'm confused about what your thinking was right from the very beginning. Your first step appears to be evaluating the limit by plugging in x = 1.1. Because the function you're taking the limit of is defined at the value x is approaching, you can perform this kind of "plug-n-chug," but x is not approaching 1.1. It is approaching 1. If we plug in the actual value we arrive at:
\(\displaystyle \displaystyle \lim _{x\to 1+}\left(3x^2+ax \right) = 3(1)^2+a(1)=a+3\)
You're given that the limit is equal to a + 2, so the final equation then becomes a + 3 = a + 2. What value(s) of a make that equation true?
\(\displaystyle \displaystyle \lim _{x\to 1+}\left(3x^2-20x \right) = 3(1)^2-20(1)=-17\) and \(\displaystyle a+2=-20+2=-18\)
Oops. That doesn't check out. That means your daughter's solution is wrong. Your solution says that -16 <= a < -6. Let's pick -10 as a nice round value in that interval.
\(\displaystyle \displaystyle \lim _{x\to 1+}\left(3x^2-10x \right) = 3(1)^2-10(1)=-7\) and \(\displaystyle a+2=-10+2=-8\)
Uh oh. That also doesn't check out. So, now that we've proven that neither your solution nor your daughter's solution is correct, let's set to finding what the correct answer actually is and why you went wrong. I'm confused about what your thinking was right from the very beginning. Your first step appears to be evaluating the limit by plugging in x = 1.1. Because the function you're taking the limit of is defined at the value x is approaching, you can perform this kind of "plug-n-chug," but x is not approaching 1.1. It is approaching 1. If we plug in the actual value we arrive at:
\(\displaystyle \displaystyle \lim _{x\to 1+}\left(3x^2+ax \right) = 3(1)^2+a(1)=a+3\)
You're given that the limit is equal to a + 2, so the final equation then becomes a + 3 = a + 2. What value(s) of a make that equation true?
There is no value of a such that 3 + a = 2 + a.The problem says find the values of "a" when "x" approaches to +1
I suspect that we can readily help you if we have the exact and complete wording of the problem.
I am wondering whether there was a typographical error in the book because the problem as written makes no sense to me at all.The exact wording was:
IF (3x^2+ax) = a+2
lim x to +1
Find the values of "a"
This problem makes sense to me
\(\displaystyle Find\ the\ values\ of\ a\ such\ that\ \displaystyle \lim_{x \rightarrow 1}(3x^2 + ax) = a + 3.\)
The answer to that problem is that a can equal any real number.