Finding the chord of a known square and circle

A

Ahatmose

New member
Joined
May 1, 2017
Messages
38
Hi all. In a square of 5 units and a circle enclosed by it what is the chord distance involved when the chord distance across equals the chord distance to the ground as in this diagram ... Is it 4 units exactly ?

test.jpg

Cheers and the second part of the question. Does a diagonal line from the top right corner of the square to the centre bottom line meet the point where the red chord hits the blue circle as in the diagram below ?

test 2.jpg

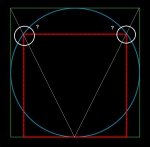
Cheers and thanks for the help.
 
Well if i coudl do it I would have not asked for help

Strange I thought I came here for some help. Regardless I will call it an exact fit and move on ... let someone, some day prove me wrong.

Cheers
 
You did get some help. ALL of the calculations you presented were reviewed for content and efficacy. Please show YOUR work. That ALWAYS works better. Then, you don't have to be frustrated.
 
A light bulb ignited

tkhunny said:
You did get some help. ALL of the calculations you presented were reviewed for content and efficacy. Please show YOUR work. That ALWAYS works better. Then, you don't have to be frustrated.
Click to expand...

Hi on looking at the image again it now seems obvious that it must be an exact fit for we have defined the two points as 4 and 3 from the origin on our x and y graph chart of the circle or centre of the square and since we know by the Pythagorean theorem that the remaining side must be 5 units it MUST BE ON THE CIRCLE. Very nice discovery of mine which shows you how to arrive at a 3, 4 5 sided right angled triangle starting with any square and it's enclosed circle. Since the diagonal line is defined by the 1 , 2 and square root of 5 triangle. Since it is 4 units up and 8 units across all prerequisites are satisfied and it is indeed an exact fit.

Cheers
Don Barone
 
If you wish, you can submit yourself to the painstaking geometrical solution.

1) Notice how the Circle is the Circumcircle of the Triangle formed by the three points of intersection with the inner square.
2) If we plaster on a Cartesian Coordinate System, with (0,0) at the bottom point of intersection, this puts the other intersections at (5/2,5) and (5/2,5).
3) One can the construct the Perpendicular Bisectors (the vertical one is particularly easy) and find the Circumcenter to be at (0,25/8).
4) This leads immediately to the Radius of the Circle, 25/8.
5) Now, we have two right triangles, the missing sides of which are each half the horizontal distance we seek.\(\displaystyle \left(\dfrac{25}{8}\right)^{2} - \left(\dfrac{15}{8}\right) = Side^{2}\)
6) A little algebra leads to \(\displaystyle Side = \dfrac{5}{2}\), which thing we already new, since we were certain two of them added up to 5 - EXACTLY!.

Here we emphasize that Unique Solutions don't care how you find them. :)
We also emphasize that there are harder ways and easier ways to go about things. :) :)
 
You must log in or register to reply here.
Top