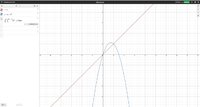
Hello guys i hope u re doing well ,im writing this post because im really confused in this case of integrals as u see in the picture the function (y= 3x-x^2 ) is above than the function (y=x),and the area is above the x-axis so why when im trying to calculate it , it gives a negative results , did i do something wrong, if no , please could u explain me why the result has a negative sign