You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Help with: A circle of radius 1 is inside a square whose side has length 2....
- Thread starter BenCurtis
- Start date
Hello, BenCurtis!
Exactly where is this second circle?
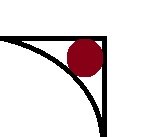
We have this diagram:A circle of radius 1 is inside a square whose side has length 2.
Show that the area of the largest circle that can be inscribed
between the circle and the square is: \(\displaystyle \pi(17-12\sqrt{2}).\)
Code:
*-------*-*-*-------* -
| * * |
| * * | :
|* *|
| | :
* *
* *---------* 2
* 1 *
| | :
|* *|
| * * | :
| * * |
*-------*-*-*-------* -
: - - - - 2 - - - - :mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
D
Deleted member 4993
Guest
I found the second circle! (It was hiding in the upper right corner.)
I sprayed it with Subhotosh paint.
View attachment 3012
Wait... Wait... that's purple - not red (color of bleeding heart liberal!!!)
Oops! Sorry for not showing work earlier.
I know that the Area of a circle is πr^(2). First, I tried to draw a 45-45-90 right triangle in the 1st Quadrant. (The origin was the middle of the circle with radius 1 and the square.) That gave me a hypotenuse of √(2). I tried to do the same thing with the circle between the first circle and the square; my goal was to divide that value by 2 and get the radius to plug into the area equation. But, as you can see from mmm444bot's sketch, there will always be a circle between the space between one circle the corner of the square. (*Even though this is a geometry-trig prob, it came out of my Dad's old calc book, so they may be looking for a limit, but I don't know for sure.*) :?:
I know that the Area of a circle is πr^(2). First, I tried to draw a 45-45-90 right triangle in the 1st Quadrant. (The origin was the middle of the circle with radius 1 and the square.) That gave me a hypotenuse of √(2). I tried to do the same thing with the circle between the first circle and the square; my goal was to divide that value by 2 and get the radius to plug into the area equation. But, as you can see from mmm444bot's sketch, there will always be a circle between the space between one circle the corner of the square. (*Even though this is a geometry-trig prob, it came out of my Dad's old calc book, so they may be looking for a limit, but I don't know for sure.*) :?:
D
Deleted member 4993
Guest
I found the second circle! (It was hiding in the upper right corner.)
I sprayed it with Subhotosh paint.
View attachment 3012
Let the corner point be C, the center of the little circle at O and the tangent points (between the little circle and the st. lines)be A and B.
Then join OA, OB and OC.
If the radius of the little circle is 'r' then OC = \(\displaystyle r\sqrt{2}\) - since OACB is a square
We also know OC = \(\displaystyle \sqrt{2} \ \ - \ \ 1 \ \ - \ \ r\)
Now go from here....
Sorry for not getting back to you sooner Subhotosh, but my question is how did you get OC = r√(2) and
OC = [FONT=MathJax_Main]2[/FONT][FONT=MathJax_Main]√[/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Math]r[/FONT]? [I do understand how OACB forms a square.]
OC = [FONT=MathJax_Main]2[/FONT][FONT=MathJax_Main]√[/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Main] [/FONT][FONT=MathJax_Math]r[/FONT]? [I do understand how OACB forms a square.]
Consider the tiny square of OACB. If r is the radius of the little circle centered at O, what is the length of the sides of OACB? So what is the length of the diagonal of that square? How does that relate to the length OC?Sorry for not getting back to you sooner Subhotosh, but my question is how did you get OC = r√(2) and
OC = [FONT=MathJax_Main]2[/FONT][FONT=MathJax_Main]√[/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Main]1[/FONT][FONT=MathJax_Main]−[/FONT][FONT=MathJax_Math]r[/FONT]? [I do understand how OACB forms a square.]
Now consider the outer square. Its sides are of length 2. So what is the length of a diagonal of the outer square?
So what is the length of the line connecting the origin to C? What is the length of the line connecting the origin to O.
I am now just explaining Subhotosh Khan's post above.Thanks JeffM. I now understand how OC = r√(2) and OC = √(2)-1-r. Now, to answer the original question, I cannot see how r = 17-12√(2) as it must since the Area of a circle = πr^(2).
You two expressions for the length of OC in terms of r and known numbers. Two numbers each equal to a third number are equal to each other. That means you can solve for r.
\(\displaystyle r\sqrt{2} = \sqrt{2} - 1 - r \implies what?\)
D
Deleted member 4993
Guest
Using the method you described, JeffM, I found that r^2 = (3-2√(2))/(3+2√(2)). [Solving for r gave me (√(2)-1)/(√(2)+1), which I then squared. I'm not sure how to break it down any more than this.]
\(\displaystyle r \ = \ \dfrac{\sqrt{2}-1}{\sqrt{2}+1}\)
multiplying right-hand-side by \(\displaystyle \dfrac{\sqrt{2}-1}{\sqrt{2}-1}\)
\(\displaystyle r \ = \ \dfrac{\sqrt{2}-1}{\sqrt{2}+1} \ * \ \dfrac{\sqrt{2}-1}{\sqrt{2}-1}\)
\(\displaystyle r \ = \ \left [{\sqrt{2}-1}\right ]^2 \ = \ 3 \ - \ 2\sqrt{2}\)
\(\displaystyle \pi \ * r^2 \ = \ \pi * \left [3 \ - \ 2\sqrt{2}\right ]^2 \ = \ ??\)
Cool, thanks Khan. I get it. By multiplying (both) sides by (√(2)-1)/(√(2)-1), you're basically just multiplying each > > > side < < by one. However, this fraction will leave a denominator of one and a numerator equal to 17-12√(2)!
BenCurtis, you are not multiplying each "side" by a form of one. That would imply each side of the equation. You are multiplying both the numerator and the denominator by that form of one.