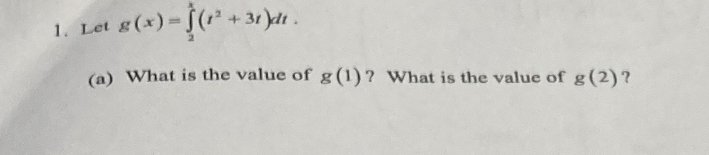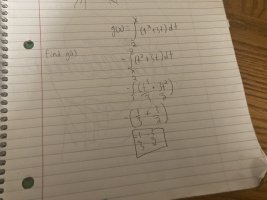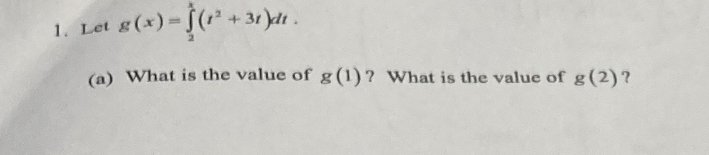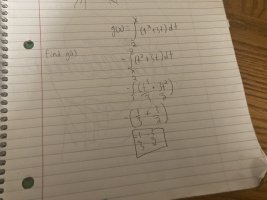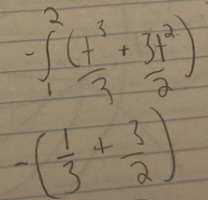khadija112
New member
- Joined
- Feb 22, 2022
- Messages
- 3
I started with negating the integral and switching the boundaries (since 1 is less than 2) then took the anti derivative. Afterwards I plugged in one for the x value and got -1/3 -3/2. I’m pretty sure I’m doing something wrong but I don’t know what.. my attempt at this problem was a guess anyways so I’m very unsure of what steps to take. Please help lol