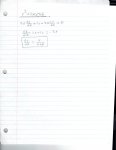You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How do I solve this seperable equation?
- Thread starter oranges
- Start date
Erm... sorry, but I don't understand what's going on here. There are four equations on your sheet and they don't really seem to be related. You say you're trying to get from the equation in the box to the underlined one, so I'll infer that the bottom equation was given in the problem statement, with the instructions to solve the differential equation for y, and the top, underlined equation is the answer given in the solution manual. But, what are the other two statements? Are they steps you've taken? Steps the solution manual took that you don't understand? Different exercises from the same unit? Something else altogether? It might be helpful if you could post the full and exact text of the problem statement, just so we'll all on the same page.
The underlined equation at the very top is what I started with. I differentiated implicitly to get the equation that I boxed off. That is the separable equation. I'm trying to work backwards now to get the equation I started with. (the underlined equation)
How do I separate the variables in the separable equation so I can get the underlined equation?
This is a problem from an old aerodynamics book with no solution manual. The underlined equation represents the equation of the streamline. The question asked for the scalar components u and v of the velocity which I solved by getting the separable equation. For fun, I want to work backwards and get the streamline equation.
So how do I solve the separable equation? (boxed equation)
Also how are they not related? I just implicitly differentiated the underlined eq to get the boxed one.
How do I separate the variables in the separable equation so I can get the underlined equation?
This is a problem from an old aerodynamics book with no solution manual. The underlined equation represents the equation of the streamline. The question asked for the scalar components u and v of the velocity which I solved by getting the separable equation. For fun, I want to work backwards and get the streamline equation.
So how do I solve the separable equation? (boxed equation)
Also how are they not related? I just implicitly differentiated the underlined eq to get the boxed one.
Last edited:
Oh, okay. I think I understand now. Those are twos, not z's. My mistake. Now that we're on the same page, let's see about running the process "in reverse." As you know, integration is the opposite of derivation. So, what happens if we start by separating out the equation? We started with:
\(\displaystyle \dfrac{dy}{dx}=-\dfrac{y}{x+y}\)
Multiply both sides by x + y:
\(\displaystyle \dfrac{dy}{dx} \cdot (x+y) =-y\)
Then bring the y over to the other side to get in a more standard form:
\(\displaystyle y + (x+y) \cdot \dfrac{dy}{dx} =0\)
Now what if we take the integral of both sides with respect to x?
\(\displaystyle \displaystyle \int \left( y + (x+y) \cdot \dfrac{dy}{dx} \right) \: dx =\int 0 \: dx\)
Try continuing from here. What do you get?
\(\displaystyle \dfrac{dy}{dx}=-\dfrac{y}{x+y}\)
Multiply both sides by x + y:
\(\displaystyle \dfrac{dy}{dx} \cdot (x+y) =-y\)
Then bring the y over to the other side to get in a more standard form:
\(\displaystyle y + (x+y) \cdot \dfrac{dy}{dx} =0\)
Now what if we take the integral of both sides with respect to x?
\(\displaystyle \displaystyle \int \left( y + (x+y) \cdot \dfrac{dy}{dx} \right) \: dx =\int 0 \: dx\)
Try continuing from here. What do you get?
Harry_the_cat
Elite Member
- Joined
- Mar 16, 2016
- Messages
- 3,784
The second line should have (2x+2y) in brackets. Then divide both sides by (2x+2y) and simplify to get what's in the box.How do I get the separable equation in the box to become the equation I have underlined? Sorry I forgot the negative sign for the y in the boxed equation.
Is that what you mean??
Last edited:
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
Your main problem, mathematically, is that you think this equation is "separable"- it isn't.