allegansveritatem
Full Member
- Joined
- Jan 10, 2018
- Messages
- 962
In looking for a video on the solution of certain types of word problem I came upon one that presented this problem:

I tried to solve this by reasoning--because I couldn't think of a formula to apply. If the tank when it is intact takes two hours to fill and when it is leaking takes two hour and another 1/3rd of an hour to fill, then every hour it loses 1/6th for an hour's worth of water, so, after 12 hours it will have lost 2 hours worth of water and the tank will be empty. But, that is not correct, at least the way the problem was worked out by the person in the video. Here is how she worked it out:
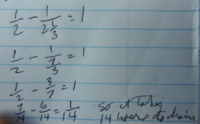
I am having a hard time getting this. The teacher presented this as a kind of black box into which you plugged in certain data and out comes the answer. She did not explain why you take the reciprocal of the time it takes to fill with a leak and subtract it from the hourly rate of the filling for the intact tank. This move does not seem intuitive to me. What happened here?

I tried to solve this by reasoning--because I couldn't think of a formula to apply. If the tank when it is intact takes two hours to fill and when it is leaking takes two hour and another 1/3rd of an hour to fill, then every hour it loses 1/6th for an hour's worth of water, so, after 12 hours it will have lost 2 hours worth of water and the tank will be empty. But, that is not correct, at least the way the problem was worked out by the person in the video. Here is how she worked it out:
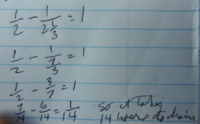
I am having a hard time getting this. The teacher presented this as a kind of black box into which you plugged in certain data and out comes the answer. She did not explain why you take the reciprocal of the time it takes to fill with a leak and subtract it from the hourly rate of the filling for the intact tank. This move does not seem intuitive to me. What happened here?

