I saw your other reply before I saw this one. This does answer some of my questions.
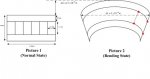
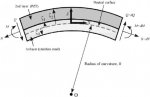
I figured out that your ∆l, which was shown as the actual width on the picture, is supposed to be only the
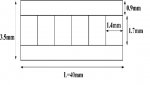
change in width. So apparently the chord is 40 mm + 5×10^-6 m (though I'd expect it to be shortened rather than lengthened!), while the height of the arc (sagitta) is 13×10^-6 m. I still don't know whether to think of the arc length as identical to the original length, but we don't need to know that. In fact, I'll ignore the ∆l, as it is insignificant in terms of significant digits.
Using the formulas from
http://mathforum.org/dr.math/faq/faq.circle.segment.html#8,
Case 8: You know
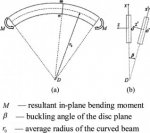
c and
h. Then
r = (c2+4h2)/(8h),
theta = 2 arcsin(c/[2r]),
s = r theta,
d = r - h,
K = r2[theta-sin(theta)]/2.
and taking c = 40×10^-3 m and h = 13×10^-6 m, we can find the radius,
r = (c^2 + 4h^2)/(8h) = (1600×10^-6 + 4×169×10^-12)/(8×13×10^-6) = 15.38 m
The angle subtended by the arc is
theta = 2 arcsin(c/[2r]) = 2 arcsin(40×10^-3/[2×15.38]) = 0.149°
Check me on the calculations!
Now, to find coordinates, you can use a little trig. The angle along the arc will be proportional to the distance along the length in the unbent form (presumably), so you can work out the angle along the arc, and use sine and cosine to find the coordinates. I don't think anything you sent shows how you want those coordinates measured, so I'm not ready to do that for you.