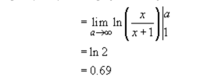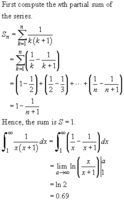You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How to find the limit of a logarithm when doing infinite series'
- Thread starter burt
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
What does the expression inside the limit equal? (Expand it as a difference of two expressions.)
The first expression approaches ln(1) = 0; the second is a constant, ln(1/2) = -ln(2).
What is the result of the subtraction?
Show us your thinking, so we can identify any errors in your work.
The first expression approaches ln(1) = 0; the second is a constant, ln(1/2) = -ln(2).
What is the result of the subtraction?
Show us your thinking, so we can identify any errors in your work.
What does the expression inside the limit equal? (Expand it as a difference of two expressions.)
The first expression approaches ln(1) = 0; the second is a constant, ln(1/2) = -ln(2).
What is the result of the subtraction?
Show us your thinking, so we can identify any errors in your work.
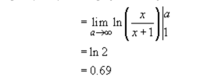 Expanding this gets: [MATH]\lim_{a\to\infty}\ln(\frac{a}{a+1})-\ln(\frac12)[/MATH]. [MATH]-\ln(\frac12)=\ln(2)[/MATH]. I wasn't sure how the rest worked, but now, as I'm writing this out again I see that the [MATH]\lim_{a\to\infty}\ln(\frac{a}{a+1})=ln(1)[/MATH] - which can be seen either with l'hopitals rule or just by realizing that the x's in the fraction will dominate. Now I understand! Thank you!
Expanding this gets: [MATH]\lim_{a\to\infty}\ln(\frac{a}{a+1})-\ln(\frac12)[/MATH]. [MATH]-\ln(\frac12)=\ln(2)[/MATH]. I wasn't sure how the rest worked, but now, as I'm writing this out again I see that the [MATH]\lim_{a\to\infty}\ln(\frac{a}{a+1})=ln(1)[/MATH] - which can be seen either with l'hopitals rule or just by realizing that the x's in the fraction will dominate. Now I understand! Thank you!Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
Exactly. And this is part of the reason we ask to see your work - so you can realize you know how!
Another way to deal with [MATH]\frac{a}{a+1}[/MATH] is to carry out the division: [MATH]\frac{a}{a+1} = 1 - \frac{1}{a+1}[/MATH].
Another way to deal with [MATH]\frac{a}{a+1}[/MATH] is to carry out the division: [MATH]\frac{a}{a+1} = 1 - \frac{1}{a+1}[/MATH].
- Joined
- Nov 24, 2012
- Messages
- 3,021
If I were faced with the limit:
[MATH]L=\lim_{a\to\infty}\left(\left.\ln\left(\frac{x}{x+1}\right)\right|_1^a\right)[/MATH]
I would work within the parentheses on the limit first:
[MATH]L=\lim_{a\to\infty}\left(\ln\left(\frac{2a}{a+1}\right)\right)[/MATH]
[MATH]L=\ln\left(\lim_{a\to\infty}\left(\frac{2}{1+\dfrac{1}{a}}\right)\right)=\ln(2)[/MATH]
[MATH]L=\lim_{a\to\infty}\left(\left.\ln\left(\frac{x}{x+1}\right)\right|_1^a\right)[/MATH]
I would work within the parentheses on the limit first:
[MATH]L=\lim_{a\to\infty}\left(\ln\left(\frac{2a}{a+1}\right)\right)[/MATH]
[MATH]L=\ln\left(\lim_{a\to\infty}\left(\frac{2}{1+\dfrac{1}{a}}\right)\right)=\ln(2)[/MATH]
HallsofIvy
Elite Member
- Joined
- Jan 27, 2012
- Messages
- 7,763
Your question is "How does \(\displaystyle \lim_{a\to \infty}\left[ln\left(\frac{x}{x+ 1}\right)\right]_1^a= 0.69\). The answer to that is "it doesn't!". That limit is ln(2) which is approximately 0.69.
In the first place, \(\displaystyle \left[ln\left(\frac{x}{x+ 1}\right)\right]_1^a\) means \(\displaystyle ln\left(\frac{a}{a+1}\right)- \ln\left(\frac{1}{1+1}\right)= ln\left(\frac{2a}{a+1}\right)\). Further, ln(x) is continuous for all positive x so this limit is the same as \(\displaystyle ln\left(\lim_{a \to\infty}\frac{2a}{a+ 1}\right)\).
To find \(\displaystyle \lim_{a \to\infty}\frac{2a}{a+ 1}\), divide both numerator and denominator by a: \(\displaystyle \frac{2a}{a+ 1}= \frac{2}{1+\frac{1}{a}}\) and, now, as a goes to infinity, 1/a goes to 0 so that limit is \(\displaystyle \frac{2}{1}= 2\). \(\displaystyle ln\left(\lim_{a \to\infty}\frac{2a}{a+ 1}\right)= ln(2)\).
In the first place, \(\displaystyle \left[ln\left(\frac{x}{x+ 1}\right)\right]_1^a\) means \(\displaystyle ln\left(\frac{a}{a+1}\right)- \ln\left(\frac{1}{1+1}\right)= ln\left(\frac{2a}{a+1}\right)\). Further, ln(x) is continuous for all positive x so this limit is the same as \(\displaystyle ln\left(\lim_{a \to\infty}\frac{2a}{a+ 1}\right)\).
To find \(\displaystyle \lim_{a \to\infty}\frac{2a}{a+ 1}\), divide both numerator and denominator by a: \(\displaystyle \frac{2a}{a+ 1}= \frac{2}{1+\frac{1}{a}}\) and, now, as a goes to infinity, 1/a goes to 0 so that limit is \(\displaystyle \frac{2}{1}= 2\). \(\displaystyle ln\left(\lim_{a \to\infty}\frac{2a}{a+ 1}\right)= ln(2)\).