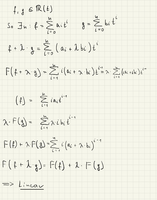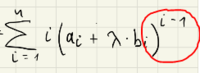How to show that formal derivative is an endomorphism?

[Frankenstein143]

In this example the formal derivative of a polynomial is given.
In (a) the want me to show that the map f-->f' on R-Vectorspace defines an Endomorpism.
In (b) they ask what is the kernel and which function (image?) has this endomorphism?

I really have difficulty even understand what and how I should show that f---->f´ is an endomorphism.
I think I have to prove it with the definition of Endomorphism:

F(af+f')=aF(f)+F(f')

Should I do this: F(af+f')=aF(f)+F(f')?
If yes, then what is F?

 

[Frankenstein143]

Here I tried to solve the Problem, What would you say?

 

[Dr.Peterson]

Here I tried to solve the Problem, What would you say?
View attachment 27795

What you're doing is appropriate; but be careful! Did you really mean this?


and this?

 

[Frankenstein143]

Sorry, I don't understand. Do you mean it is false to take lambda out?
And what is wrong with i-1? The map is f--->f' so that F is the derivative, therefore I took derivative.

I do not understand this Example at all, please give me the right solution so that I can compare it.

 

[Frankenstein143]

Oh I forgot to write the "t"

 

[Dr.Peterson]

Sorry, I don't understand. Do you mean it is false to take lambda out?

You didn't actually use the rewritten form, which is good.

Lambda is not a factor of both terms, so of course you can't factor it out.

Oh I forgot to write the "t"

Yes, that was my point: Be careful to write what you mean.

 

[Frankenstein143]

Thank you!
What is about (b)? what kernel and which function (image?) have this endomorphism?
I have little time left and have to submit my sheet, so if someone can please give me the solution for (b)

 

[Dr.Peterson]

Thank you!
What is about (b)? what kernel and which function (image?) have this endomorphism?
I have little time left and have to submit my sheet, so if someone can please give me the solution for (b)

I believe it's asking for the kernel and the image of the endomorphism defined by the formal derivative.

What is the definition of kernel? Apply it.

What is the definition of image? Apply it.

Then tell us what you think. These are not hard, though the second may take a little thought to see why it is not the entire vector space. (Then you'll wonder why it took so long to see.)