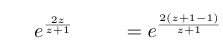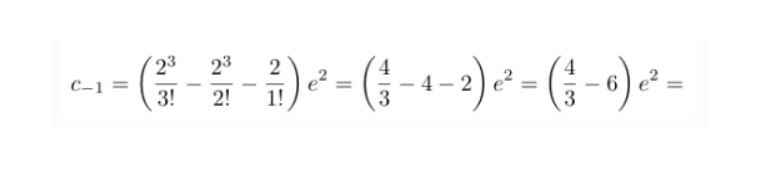[math]\int_Γ z^2e^{2z/(z+1)} dz[/math]
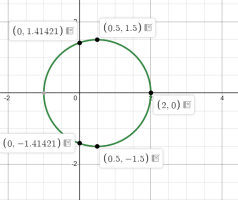
[math]|z-\frac{1}{2}|=R[/math]
[math]R\neq\frac{3}{2}[/math]
[math]R>0[/math]
I know to use the modulus and get the points at x and y and plot them but what I want to find out is how does the radius R descreases and increases by 3/2 as [math]R<3/2[/math] and [math]R>3/2[/math]?
How does this interval appears?
Also in my contest textbook for complex analysis how does the first condition which is smaller by 3/2 makes the integral 0?
I know that the pole is [math]z_0=-1[/math] because [math]z_0+1=0[/math]It's in roumanian but it says that there are 2 cases
If [math]R<3/2[/math]
[math]I=0[/math]
If [math]R>3/2[/math]
[math]I=2*\pi*i*Rez(g,-1)[/math]
When I tried to use the integral I got [math]\int_Γ\frac{2z}{(z+1)^2}[/math].Is it wrong?I used the formula [math]\frac{1}{2*\pi*i}\int_Γ\frac{f(z)}{z-z0}[/math]where [math]f(z)=\frac{2z}{z+1}[/math]
Also can someone explain why
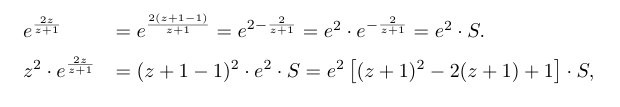
and
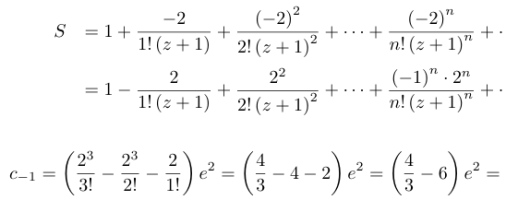
This is what I did

Can someone please explain me how to apply the Laurent series in my problem?
I have a few courses in romanian and there are not a lot of romanians here but I'm participating in a student competition of complex analysis(Traian Lalescu)
[math]|z-\frac{1}{2}|=R[/math]
[math]R\neq\frac{3}{2}[/math]
[math]R>0[/math]
I know to use the modulus and get the points at x and y and plot them but what I want to find out is how does the radius R descreases and increases by 3/2 as [math]R<3/2[/math] and [math]R>3/2[/math]?
How does this interval appears?
Also in my contest textbook for complex analysis how does the first condition which is smaller by 3/2 makes the integral 0?
I know that the pole is [math]z_0=-1[/math] because [math]z_0+1=0[/math]It's in roumanian but it says that there are 2 cases
If [math]R<3/2[/math]
[math]I=0[/math]
If [math]R>3/2[/math]
[math]I=2*\pi*i*Rez(g,-1)[/math]
When I tried to use the integral I got [math]\int_Γ\frac{2z}{(z+1)^2}[/math].Is it wrong?I used the formula [math]\frac{1}{2*\pi*i}\int_Γ\frac{f(z)}{z-z0}[/math]where [math]f(z)=\frac{2z}{z+1}[/math]
Also can someone explain why
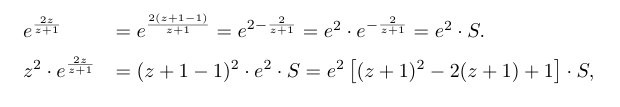
and
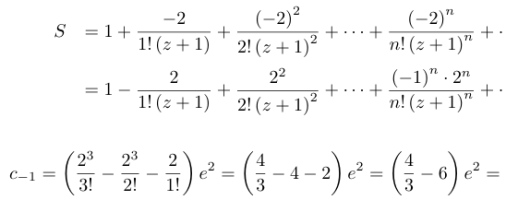
This is what I did

Can someone please explain me how to apply the Laurent series in my problem?
I have a few courses in romanian and there are not a lot of romanians here but I'm participating in a student competition of complex analysis(Traian Lalescu)
Attachments
Last edited: