NotGreatAtMath
New member
- Joined
- Nov 21, 2019
- Messages
- 4
So there is this hard problem I tried to solve, but I had no idea what to do.
The problem:
There are
8 Greek
10 American
15 Russian
16 Chinese
22 Canadian students.
Students study in groups.
A group is made up from one or more students.
If there are two or more students of the same nationality in a group, there must be at least one student of another nationality in the group.
In how many ways can 71 students divide the group?
I guess I should do some combination stuff
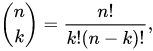 Maybe use this fancy formula. idk.
Maybe use this fancy formula. idk.
I'm totally lost, any help would be appreciated
The problem:
There are
8 Greek
10 American
15 Russian
16 Chinese
22 Canadian students.
Students study in groups.
A group is made up from one or more students.
If there are two or more students of the same nationality in a group, there must be at least one student of another nationality in the group.
In how many ways can 71 students divide the group?
I guess I should do some combination stuff
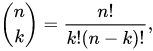 Maybe use this fancy formula. idk.
Maybe use this fancy formula. idk.I'm totally lost, any help would be appreciated
