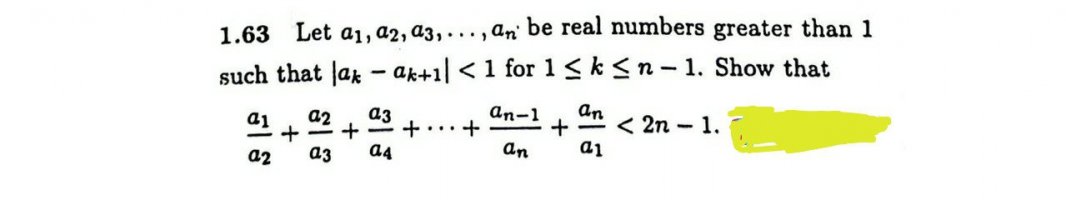You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Inequality Problem
- Thread starter AdkAdi
- Start date
D
Deleted member 4993
Guest
Why is part of your question masked out with yellow?View attachment 28850
I tried using Am-Gm inequality but that approach did not yield anything significant.
Why do you not try induction on such problems?
[math]\text {ASSUME } n = 2.[/math]
[math]\text {It is true by hypothesis that } 1 < a_1 \text { and } 1 < a_2.[/math]
[math]\text {Case I: } 1 < a_1 \le a_2 \implies \dfrac{a_1}{a_2} \le 1\implies \\ \dfrac{a_1}{a_2} < 3 = 4 - 1 = 2n - 1.[/math]
[math]\text {Case II: } a_1 > a_2 > 1 \implies a_1 - a_2 < 0 \implies |a_2 - a_1| = a_1 - a_2 > 0.\\ \therefore 0 < a_1 - a_2 < 1 \ \because \ |a_2 - a_1| < 1.\\ \therefore a_2 < a_1 < a_2 + 1 \implies 1 < \dfrac{a_1}{a_2} < 1 + \dfrac{1}{a_2} < 2 \ \because \ 1 < a_2 \text { by hypothesis.}\\ \therefore \dfrac{a_1}{a_2} < 3 = 2n - 1.[/math]
So we can prove the proposition is true if n = 2.
Now what?
[math]\text {ASSUME } n = 2.[/math]
[math]\text {It is true by hypothesis that } 1 < a_1 \text { and } 1 < a_2.[/math]
[math]\text {Case I: } 1 < a_1 \le a_2 \implies \dfrac{a_1}{a_2} \le 1\implies \\ \dfrac{a_1}{a_2} < 3 = 4 - 1 = 2n - 1.[/math]
[math]\text {Case II: } a_1 > a_2 > 1 \implies a_1 - a_2 < 0 \implies |a_2 - a_1| = a_1 - a_2 > 0.\\ \therefore 0 < a_1 - a_2 < 1 \ \because \ |a_2 - a_1| < 1.\\ \therefore a_2 < a_1 < a_2 + 1 \implies 1 < \dfrac{a_1}{a_2} < 1 + \dfrac{1}{a_2} < 2 \ \because \ 1 < a_2 \text { by hypothesis.}\\ \therefore \dfrac{a_1}{a_2} < 3 = 2n - 1.[/math]
So we can prove the proposition is true if n = 2.
Now what?