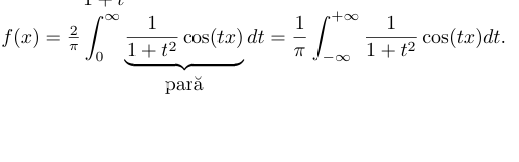In my book This exercise îs solved by Jordan lemma and I Don't know how to apply it
I will explain to you the idea of the Jordan lemma. If you solve integrals in complex analysis, you use a contour (path). This contour splits the original integral into two or more integrals. One of these integrals involves an arc (usually an arc of a semicircle). The Jordan lemma says that the integral that involves the arc \(\displaystyle = 0\). That's the whole idea.
Now let us apply it step by step.
[math]g(z)= \frac{e^{izx}}{z^2+1}[/math]?
First step is that we have to define our complex function.
Let our complex function be \(\displaystyle g(z)= \frac{e^{izx}}{z^2+1}\).
We realize that this function has two poles \(\displaystyle z = i\) and \(\displaystyle z = -i\)
Step 2. We will choose a contour. Let our contour be \(\displaystyle \gamma\). We will let this contour contains only one of the poles. What about the top part of a semicircle of radius \(\displaystyle R\) and \(\displaystyle R > 1\). This means that the pole \(\displaystyle z = i\) will be inside the contour (the semicircle) and we can compute its residue.
This is our contour: We will walk from \(\displaystyle z = -R\) to \(\displaystyle z = R\) (real line), then from \(\displaystyle z = R\) back to \(\displaystyle z = -R\) through the semicircular arc which we will call \(\displaystyle \gamma_R\). As you can see, our contour is perfectly closed.
Then, our integral is:
\(\displaystyle \int_{\gamma} g(z) \ dz = \int_{-R}^{R} g(z) \ dz + \int_{\gamma_R} g(z) \ dz\)
Step 3. Apply the residue theorem.
\(\displaystyle \int_{\gamma} g(z) \ dz = 2\pi i \cdot \text{Res}(g,i)\)
This means that:
\(\displaystyle \int_{-R}^{R} g(z) \ dz + \int_{\gamma_R} g(z) \ dz = 2\pi i \cdot \text{Res}(g,i)\)
Step 4. Apply the limit to both sides.
\(\displaystyle \lim_{R \rightarrow \infty}\int_{-R}^{R} g(z) \ dz + \lim_{R \rightarrow \infty} \int_{\gamma_R} g(z) \ dz = \lim_{R \rightarrow \infty} 2\pi i \cdot \text{Res}(g,i)\)
Step 5. Use the Jordan lemma.
\(\displaystyle \lim_{R \rightarrow \infty} \int_{\gamma_R} g(z) \ dz = 0\)
Then,
\(\displaystyle \lim_{R \rightarrow \infty}\int_{-R}^{R} g(z) \ dz = \lim_{R \rightarrow \infty} 2\pi i \cdot \text{Res}(g,i)\)
Or
\(\displaystyle \lim_{R \rightarrow \infty}\int_{-R}^{R} g(z) \ dz = 2\pi i \cdot \text{Res}(g,i)\)
Step 6. Calculate the residue.
\(\displaystyle \text{Res}(g,i) = \frac{e^{-x}}{2i}\)
Then,
\(\displaystyle \lim_{R \rightarrow \infty}\int_{-R}^{R} g(z) \ dz = \pi e^{-x}\)
Or
\(\displaystyle \int_{\gamma} g(z) \ dz = \lim_{R \rightarrow \infty}\int_{-R}^{R} g(z) \ dz = \pi e^{-x}\)
Or
\(\displaystyle \int_{-\infty}^{\infty} \frac{e^{izx}}{z^2 + 1} \ dz = \pi e^{-x}\)
Since we have chosen the contour as the upper half of the semicircle, we were actually calculating only \(\displaystyle x > 0\).
In other words, we were calculating the cosine Fourier transform.
Then,
\(\displaystyle \int_{-\infty}^{\infty}\frac{\cos(xz)}{z^2 + 1} \ dz = \text{Re}\left(\int_{-\infty}^{\infty} \frac{e^{izx}}{z^2 + 1} \ dz\right) = \pi e^{-x}\)
Or
\(\displaystyle \frac{1}{\pi}\int_{-\infty}^{\infty}\frac{\cos(xz)}{z^2 + 1} \ dz = e^{-x}\)
The same result we have obtained in post #\(\displaystyle 8\).
Now if you wanna calculate \(\displaystyle x < 0\) using the Jordan lemma, you do the same calculations we have done but you choose your contour to be the bottom part of the semicircle.
You will get: \(\displaystyle \int_{-\infty}^{\infty} \frac{e^{izx}}{z^2 + 1} \ dz = \pi e^{x}\)
And by combining the two solutions together, you will get again:
\(\displaystyle f(x) = \mathcal{F^{-1}}\left\{\frac{1}{z^2 + 1}\right\} =\begin{cases}e^{-x} & x > 0\\e^{x} & x < 0\end{cases} = e^{-|x|}\)