Ihatdogs10
Junior Member
- Joined
- May 19, 2021
- Messages
- 91
Greetings can someone help me to solve it?
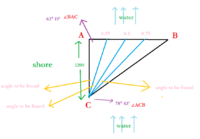
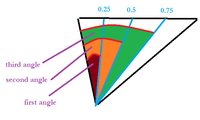
A and B are two points on opposite sides of a body of water, and soundings are to be taken in the line AB at points one quarter, one half, and three quarters of the distance from A to B. On the shore, a line AC 1200 feet long is measured, and angles BAC = 63° 19' and ACB = 78° 43'. What angles must be turned off from CA at C in order to line up the boat from which the soundings are made at the proper points on AB?
A and B are two points on opposite sides of a body of water, and soundings are to be taken in the line AB at points one quarter, one half, and three quarters of the distance from A to B. On the shore, a line AC 1200 feet long is measured, and angles BAC = 63° 19' and ACB = 78° 43'. What angles must be turned off from CA at C in order to line up the boat from which the soundings are made at the proper points on AB?