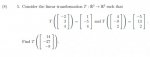Linear Transformation: T([-2,3,4])=[1,-5,4], T([4,-9,2])=[-5,13,2]; find T([14,-27,-8

[AjaxPro]

5. Consider the linear transformation \(\displaystyle T\, :\, \mathbb{R}^3\, \rightarrow\, \mathbb{R}^3\) such that

. . . . .\(\displaystyle \displaystyle T\,\left(\left[\begin{array}{r}-2\\3\\4\end{array}\right]\right)\, =\, \left[\begin{array}{r}1\\-5\\4\end{array}\right]\)

and

. . . . .\(\displaystyle \displaystyle T\,\left(\left[\begin{array}{r}4\\-9\\2\end{array}\right]\right)\, =\, \left[\begin{array}{r}-5\\13\\2\end{array}\right]\)

Find

. . . . .\(\displaystyle \displaystyle T\,\left(\left[\begin{array}{r}14\\-27\\-8\end{array}\right]\right)\)

---

Hi I am new to this website.

I am currently trying to work on figuring out how to do Linear Transformations. Can anyone help guide me in the right direction?

 

[HallsofIvy]

Since you are given the result of applying the linear transformation to \(\displaystyle \begin{bmatrix}-2 \\ 3 \\ 4 \end{bmatrix}\) and \(\displaystyle \begin{bmatrix}4 \\ -9 \\ 2\end{bmatrix}\) you want to write this vector as a linear combination of them. That is, you want to find numbers a and b such that \(\displaystyle \begin{bmatrix}14 \\ -27 \\ -8\end{bmatrix}= a\begin{bmatrix}-2 \\ 3 \\ 4 \end{bmatrix}+ b\begin{bmatrix}4 \\ -9 \\ 2\end{bmatrix}\). Of course that is the same as \(\displaystyle \begin{bmatrix}14 \\ -27 \\ -8\end{bmatrix}= \begin{bmatrix}-2a \\ 3a \\ 4a \end{bmatrix}+ \begin{bmatrix}4b \\ -9b \\ 2b\end{bmatrix}\) so that a and b must satisfy 14=-2a+ 4b, -27= 3a- 9b, and -8= 4a+ 2b. That is three equations in two unknown values so there may not be a solution! If there is then use the fact that, for a linear transformation, T, T(au+ bv)= aT(u)+ bT(v).