Log-likelihood function

[bleh]

Hi, I am trying to solve a time series problem but I am stuck with a function I am not used to work with. I have a basic yt=d +B(yt-1)+e(t) model where e(t) has mean 0 and variance sigma^2. The issue is that (e)t follows the density function.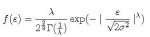


It's causing me issues because of the gamma function with the (1/L) after. Does anyone know how I need to handle that part of the function to build my log likelihood function for (d,B,o^2) ? What I have tried so far has let me with the following: L=Lambda (is a known parameter), G=gamma function, o is sigma

-2/3 ln 2L - ln G(1/L) - Sum(t=2, T) (yt-d-B(yt-1))^L/(2o^2)^(1/2) - (y1-d/(1-B))^L / (2o^2/(1-B^2))^(1/2)

Is this way of handling the density function with the Gamma correct (basically ignoring it as it goes away after the derivatives)? If not could anyone shed some light on the way I should approach this to solve it?

Thanks a lot.

 

[tkhunny]

That's fine, but at some point you should notice that given a constant \(\displaystyle \lambda\), you have a constant \(\displaystyle \Gamma\left(\frac{1}{\lambda}\right)\). When you get around to the derivative, it wil go away.