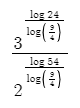You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
logarithm simplification
- Thread starter 5ugxr
- Start date
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,849
Wolfram Alpha does give 2.4494897..., which is [imath]\sqrt{6}[/imath]; but it doesn't simplify it to that expression, suggesting that this isn't particularly easy ...View attachment 38369
I'm having trouble with simplifying this logarithmic expression to sqrt6, anything I try keeps getting messed up because of the different bases and the different exponents. I also tried rewriting 24 as 3 * 2^3 and 54 as 2 * 3^3 but I wasn't able to simplify
Yea, I was trying to find some online calculators to simplify it but they all keep giving me answers in logarithmic form...Wolfram Alpha does give 2.4494897..., which is [imath]\sqrt{6}[/imath]; but it doesn't simplify it to that expression, suggesting that this isn't particularly easy ...
My teacher said I have to use exponent and logarithm laws to simplify (that's a given...) but I'm not seeing any way to do it
What do you get - in log form & NOT in decimal form - when you simplify:View attachment 38369
I'm having trouble with simplifying this logarithmic expression to sqrt6, anything I try keeps getting messed up because of the different bases and the different exponents. I also tried rewriting 24 as 3 * 2^3 and 54 as 2 * 3^3 but I wasn't able to simplify
\(\displaystyle \dfrac{\log{24}}{\log({\frac{9}{4})}}\)
Log base 9/4 of 24?What do you get - in log form & NOT in decimal form - when you simplify:
\(\displaystyle \dfrac{\log{24}}{\log({\frac{9}{4})}}\)
Incorrect - how did you get that?Log base 9/4 of 24?
Start with:
log (9/4) ............ the base of "log" here is assumed to be 10 , according to common convention
log(9/4) = log(9) - log(4) = 2 * log(3) - 2 * log(2).................. and
log(24) = log(3*2 * 2*2) = log(3) + 3*log(2)
Oh, yes I understand thatIncorrect - how did you get that?
Start with:
log (9/4) ............ the base of "log" here is assumed to be 10 , according to common convention
log(9/4) = log(9) - log(4) = 2 * log(3) - 2 * log(2).................. and
log(24) = log(3*2 * 2*2) = log(3) + 3*log(2)
I thought this was expanding it haha, I can see your steps tho
I was a bit confused, it was log(a)/log(b) so I was just thinking change of base rule
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
This is unorthodox of the site but here's my solution.
[math]\frac{3^{\log(24)/ \log(9/4)}}{2^{\log(54)/\log(9/4)}} = x; \text{where } x > 0 [/math][math]\dfrac{3 \log(2) + \log(3)}{2 \log(3/2)}\log 3 -\dfrac{\log(2) + 3 \log(3)}{2 \log(3/2)}\log 2= \log x[/math][math]\dfrac{(\log(3))^2-(\log(2))^2}{2 \log(3/2)}= \log x[/math][math]\dfrac{(\log(3)+\log(2))(\log(3)-\log(2))}{2(\log(3)-\log(2))}= \log x[/math][math]\dfrac{\log(3)+\log(2)}{2}= \log x[/math][math]\log(6) = \log(x^2)[/math][math]6=x^2[/math][math]x=\sqrt{6}[/math]
I came up to the same idea, but you were faster.This is unorthodox of the site but here's my solution.
[math]\frac{3^{\log(24)/ \log(9/4)}}{2^{\log(54)/\log(9/4)}} = x; \text{where } x > 0 [/math][math]\dfrac{3 \log(2) + \log(3)}{2 \log(3/2)}\log 3 -\dfrac{\log(2) + 3 \log(3)}{2 \log(3/2)}\log 2= \log x[/math][math]\dfrac{(\log(3))^2-(\log(2))^2}{2 \log(3/2)}= \log x[/math][math]\dfrac{(\log(3)+\log(2))(\log(3)-\log(2))}{2(\log(3)-\log(2))}= \log x[/math][math]\dfrac{\log(3)+\log(2)}{2}= \log x[/math][math]\log(6) = \log(x^2)[/math][math]6=x^2[/math][math]x=\sqrt{6}[/math]
Much simpler than my way. I was simplifying the given expression and replace log(3)= A and log(2)=B and then simplify further as algebraic expression. After 3 pages - came to the same point.This is unorthodox of the site but here's my solution.
[math]\frac{3^{\log(24)/ \log(9/4)}}{2^{\log(54)/\log(9/4)}} = x; \text{where } x > 0 [/math][math]\dfrac{3 \log(2) + \log(3)}{2 \log(3/2)}\log 3 -\dfrac{\log(2) + 3 \log(3)}{2 \log(3/2)}\log 2= \log x[/math][math]\dfrac{(\log(3))^2-(\log(2))^2}{2 \log(3/2)}= \log x[/math][math]\dfrac{(\log(3)+\log(2))(\log(3)-\log(2))}{2(\log(3)-\log(2))}= \log x[/math][math]\dfrac{\log(3)+\log(2)}{2}= \log x[/math][math]\log(6) = \log(x^2)[/math][math]6=x^2[/math][math]x=\sqrt{6}[/math]
BigBeachBanana
Senior Member
- Joined
- Nov 19, 2021
- Messages
- 2,277
Though my way is shorter, 3 pages is the way to go.After 3 pages - came to the same point.
Professor Khan,Much simpler than my way. I was simplifying the given expression and replace log(3)= A and log(2)=B and then simplify further as algebraic expression. After 3 pages - came to the same point.
Can you please show us your three pages of solution?
BBB has already shown the correct (and pithy) solution and I do not want to waste time.Professor Khan,
Can you please show us your three pages of solution?