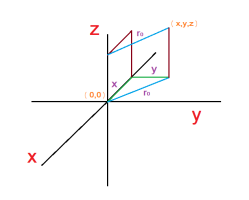
Let us start this problem with a sketch. We will rotate the solid sphere around the \(\displaystyle z\)-axis. Let us draw a line \(\displaystyle \textcolor{purple}{r_0}\) on the \(\displaystyle x\)-\(\displaystyle y\) plane that is perpendicular to the axis of rotation (\(\displaystyle z\)-axis). If we move this line \(\displaystyle \textcolor{purple}{r_0}\) in space, it is still perpendicular and has the same distance to the axis of rotation as shown in the sketch. If the point \(\displaystyle (x,y,z)\) is on the edge of a sphere (centered at the origin) of radius \(\displaystyle r\), then we can express the distance \(\displaystyle \textcolor{purple}{r_0}\) in terms of \(\displaystyle r\) and \(\displaystyle z\), as shown below:
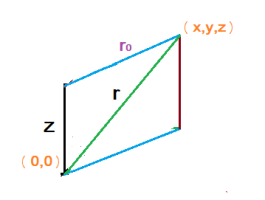
\(\displaystyle \textcolor{purple}{r_0^2} = r^2 - z^2\)
Or
\(\displaystyle \textcolor{purple}{r_0} = \sqrt{r^2 - z^2}\)
This is the perpendicular distance between any mass inside the solid sphere and the axis of rotation.
Then, we have:
\(\displaystyle I_z = \int R^2 \ dm = \int r_0^2 \ dm = \int (r^2 - z^2) \ dm\)
Finding \(\displaystyle \textcolor{purple}{r_0}\) was the most difficult part. Now, the rest is trivial.
\(\displaystyle I_z = \int (r^2 - z^2) \ dm = \int (r^2 - z^2) \rho \ dV = \int\int\int (r^2 - z^2) \rho \ r^2 \sin \phi \ dr \ d\phi \ d\theta\)
\(\displaystyle z = r\cos \phi\) in the spherical coordinate.
\(\displaystyle I_z = \int\int\int (r^2 - r^2\cos^2\phi) \rho \ r^2 \sin \phi \ dr \ d\phi \ d\theta = \int_{0}^{2\pi}\int_{0}^{\pi}\int_{0}^{R} r^4 \rho \ (1 - \cos^2 \phi)\sin \phi \ dr \ d\phi \ d\theta\)
\(\displaystyle = \int_{0}^{2\pi}\int_{0}^{\pi} \frac{R^5}{5} \rho \ (1 - \cos^2 \phi)\sin \phi \ d\phi \ d\theta = \int_{0}^{\pi} 2\pi\frac{R^5}{5} \rho \ (1 - \cos^2 \phi)\sin \phi \ d\phi\)
\(\displaystyle = 2\pi\frac{R^5}{5} \rho \left(\frac{\cos^3\phi}{3} - \cos \phi\right)\bigg|_{0}^{\pi} = 2\pi\frac{R^5}{5} \rho \left(\frac{\cos^3\pi}{3} - \cos \pi - \frac{\cos^{3}0}{3} + \cos 0\right)\)
\(\displaystyle = 2\pi\frac{R^5}{5} \rho \left(-\frac{1}{3} - (-1) - \frac{1}{3} + 1\right) = 2\pi\frac{R^5}{5} \rho \left(-\frac{2}{3} + 2\right) = 8\pi\frac{R^5}{15} \rho\)
We know that the volume density \(\displaystyle \rho = \frac{M}{V} = \frac{M}{\frac{4}{3}\pi R^3}\), then
\(\displaystyle I_z = 8\pi\frac{R^5}{15} \rho = 8\pi\frac{R^5}{15}\frac{M}{\frac{4}{3}\pi R^3} = \textcolor{blue}{\frac{2}{5}MR^2}\)





