Moved _ Triangles

[procrasterbate]

Hi, i need some help finding a area formula of a triangle give only a angle (Theta) and the height (actually the radius of a circle that the triangle is circumscribed, denoted R). Also the angle given is the unique angle of the triangle.

 

[Unknown008]

I'm a little confused about the triangle. Are all its vertices on the circumference of the circle? It would be helpful if you can give the vertices labels, like A, B and C, and say what the angle is, where are each point in the circle.

EDIT: Doesn't this question conform more to 'Geometry' than 'Calculus'?

 

[Bob Brown MSEE]

Hi, i need some help finding a area formula of a triangle give only a angle (Theta) and the height (actually the radius of a circle that the triangle is circumscribed, denoted R). Also the angle given is the unique angle of the triangle.

If the height of a circumscribed triangle is the radius then the angle must be 45 degrees.
I also do not understand the question. Can you insert a picture?

 

[procrasterbate]

pic

 

[Unknown008]

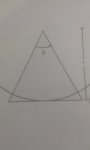
Okay, since you don't have any values as such, I am assuming that you're required to get the area of the triangle in terms of \(\displaystyle \theta\) and \(\displaystyle r\).

You know that the height is \(\displaystyle r\).

Let's name the top vertex as \(\displaystyle A\) and the two vertices be \(\displaystyle B\) and \(\displaystyle C\) respectively and the point where the circle touches the base of the triangle be \(\displaystyle D\)

Then, \(\displaystyle \widehat{BAD} = \dfrac{\theta}{2}\) and \(\displaystyle \widehat{ADB} = 90^o\)

This means that we have a right angled triangle and we can use trigonometry to get the sides AB and BD. What interests us here is the base, since we know that the height is \(\displaystyle r\), hence we want to know \(\displaystyle BD\)

\(\displaystyle BD = \dfrac{AD}{\tan\left(\dfrac{\theta}{2}\right)}\)

\(\displaystyle BC\) is simply twice this.

\(\displaystyle BC = \dfrac{2AD}{\tan\left(\dfrac{\theta}{2}\right)}\)

Can you find the area of the triangle now?

EDIT: Not sure how to turn off the automatic parsing link of 'angle'...