Thank you for that.
I had assumed it might require the use of double integration (as I'd seen discussed here) but I'll take your word for it that what you've shown does the job. It does produce a result (34 cubic yards) in nearly the same 'ball-park' as I got with my geometric approximation so I guess I'm happy. 
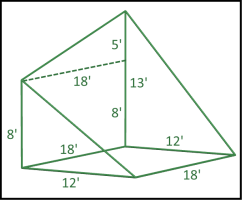
Here is my approach.
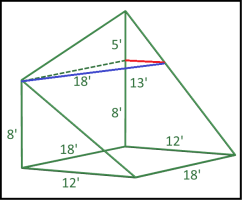
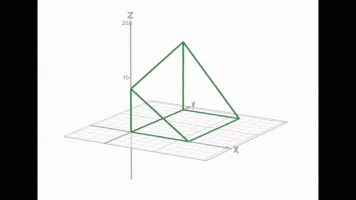
Look at my diagram. I reversed the shape so that I have positive values. The volume will not be affected.
My goal is to represent the
height which is shown with a formula. If I move in space from the point \(\displaystyle (0,0,8)\) to \(\displaystyle (18,0,13)\) I can parametrize this segment by \(\displaystyle r(t) = (0,0,8) + t(18 - 0, 0 - 0, 13 - 8) = (0,0,8) + (18t,0,5t) = (18t,0,8 + 5t)\).
Thanks to the differential geometry!
This gives:
\(\displaystyle x(t) = 18t\)
\(\displaystyle y(t) = 0\)
\(\displaystyle z(t) = 8 + 5t\)
Therefore, the height of this prism's face (along the \(\displaystyle x\)-axis) is always \(\displaystyle z(t) = 8 + 5t\). Now we will take a slice of the volume of this prism (the pink volume) and increase it to the full \(\displaystyle y\)-axis, the face along the \(\displaystyle y\)-axis is just a triangle. So, the volume of this new slice (increased slice) is just \(\displaystyle \frac{1}{2}12z \ dx\).
We can write the volume of the prism with triple integrals like this:
\(\displaystyle V = \int dV = \frac{1}{2}\int_{0}^{18}\int_{0}^{12}\int_{0}^{z} dz \ dy \ dx\)
Or directly like this:
\(\displaystyle V = \frac{1}{2}\int_{0}^{18} 12z \ dx = \int_{0}^{18}6(8 + 5t) \ dx\)
We know that \(\displaystyle x = 18t\), then \(\displaystyle t = \frac{x}{18}\).
This gives:
\(\displaystyle V = 6\int_{0}^{18}\left(8 + \frac{5x}{18}\right) \ dx = 1134 \ \text{unit}^3\)
I got a different result this time because in the last post I wrote \(\displaystyle 8 + \frac{5x}{18}\) as \(\displaystyle 8 + \frac{x}{18}\), forgetting to multiply \(\displaystyle x\) by \(\displaystyle 5\).