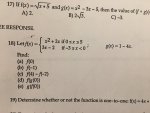Piecewise Function: f(x) = x^2+2x for 0<=x<=5, 3x-2 for -3<=x<0; g(x) = 1-4x
Hey everyone, I've been trying to figure this problem out for hours now!
18) Let \(\displaystyle \,f(x)\, =\, \begin{cases}x^2\, +\, 2x & \mbox{if }\, 0\, \leq\, x\, \leq\, 5 \\ 3x\, -\, 2 & \mbox{if }\, -3\, \leq\, x\, <\, 0 \end{cases}\,\) and \(\displaystyle \,g(x)\, =\, 1\, -\, 4x\)
. . . . .Find:
. . . . .(a) f (0)
. . . . .(b) f (-1)
. . . . .(c) f (4) - f (-2)
. . . . .(d) f (g (0))
. . . . .(e) g (f (0))
Can anyone help? Thank you!!
Hey everyone, I've been trying to figure this problem out for hours now!
18) Let \(\displaystyle \,f(x)\, =\, \begin{cases}x^2\, +\, 2x & \mbox{if }\, 0\, \leq\, x\, \leq\, 5 \\ 3x\, -\, 2 & \mbox{if }\, -3\, \leq\, x\, <\, 0 \end{cases}\,\) and \(\displaystyle \,g(x)\, =\, 1\, -\, 4x\)
. . . . .Find:
. . . . .(a) f (0)
. . . . .(b) f (-1)
. . . . .(c) f (4) - f (-2)
. . . . .(d) f (g (0))
. . . . .(e) g (f (0))
Can anyone help? Thank you!!
Attachments
Last edited by a moderator: