Hello! The question I'm about to ask is not actually my problem. I agreed to help a friend, and it turns out I have absolutely no idea what to do either. This friend is in pre-calculus, but from what I can tell, this looks more like a problem for this section.
I do not have the actual picture for the problem as I can't access my friend's online book, so I'll try to explain it as best I can.

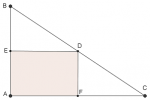
The rectangle in the middle is actually a square with sides = 5.
The Hypotenuse of the triangle ABC is 15.
Angle EBD is congruent with angle FDC.
Find side BE and FC. (BE ≠ FC)
Can the law of sines be used to solve this problem? And if so, where do you begin?
I do not have the actual picture for the problem as I can't access my friend's online book, so I'll try to explain it as best I can.
The rectangle in the middle is actually a square with sides = 5.
The Hypotenuse of the triangle ABC is 15.
Angle EBD is congruent with angle FDC.
Find side BE and FC. (BE ≠ FC)
Can the law of sines be used to solve this problem? And if so, where do you begin?
Attachments
Last edited: