HATLEY1997
Junior Member
- Joined
- Oct 24, 2023
- Messages
- 59
For Part C, you have two points:For part c, I have found that 0.0175i is added on per second however the j-value only changes slightly and is different each time. Is there somewhere I am going wrong or am I okay to round it?
Thank youFor Part C, you have two points:
[imath](1,3)[/imath] and [imath](1+\sin t,3-\cos t)[/imath]
The first point is fixed while the second point is changing, but the distance between them is always [imath]1[/imath].
Proof: use the distance formula.
[imath]d = \sqrt{(1+\sin t - 1)^2 + (3-\cos t - 3)^2} = \sqrt{(\sin t)^2 + (-\cos t)^2} = \sqrt{1} = 1[/imath]
It does not matter what is the time. Let us take a random time, [imath]t = 5[/imath].
[imath]d = \sqrt{(1+\sin 5 - 1)^2 + (3-\cos 5 - 3)^2} = \sqrt{(\sin 5)^2 + (-\cos 5)^2} = \sqrt{1} = 1[/imath]
Although this is irrelevant to the question itself, I notice that you are taking sines and cosines in degree mode, rather than radians, which is assumed for a problem like this. [imath]\sin(1rad) = 0.84147\dots[/imath]; [imath]\sin(1^\circ) = 0.01745...\dots[/imath]For part c, I have found that 0.0175i is added on per second however the j-value only changes slightly and is different each time. Is there somewhere I am going wrong or am I okay to round it?
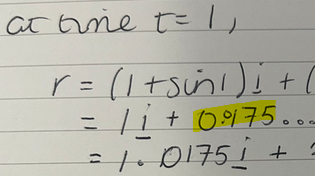
That’s really helpful and something I forgot to change on my calculator. Thank youAlthough this is irrelevant to the question itself, I notice that you are taking sines and cosines in degree mode, rather than radians, which is assumed for a problem like this. [imath]\sin(1rad) = 0.84147\dots[/imath]; [imath]\sin(1^\circ) = 0.01745...\dots[/imath]
View attachment 38478
