financestudent
New member
- Joined
- Dec 6, 2020
- Messages
- 4
Hello everybody, I am new here 
My first post concerns the evaluation of multiasset options in Robust Programming like you see from papers below
where
1) Gamma is a predefined parameter whose value reflects the degree of risk-tolerance of the investor, but for purposes of question it doesn't matter knowing what it means.
2)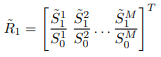 represents the vector of random returns for the first period (i.e. t=1) given the current price of m-th stock included in the underlying basket of multiasset option, for m=1,...,M.
represents the vector of random returns for the first period (i.e. t=1) given the current price of m-th stock included in the underlying basket of multiasset option, for m=1,...,M.
3)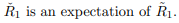 i.e. to say represents the vector of expected returns for the first period (i.e. t=1) given the current price of m-th stock included in the underlying basket of multiasset option, for m=1,...,M.
i.e. to say represents the vector of expected returns for the first period (i.e. t=1) given the current price of m-th stock included in the underlying basket of multiasset option, for m=1,...,M.
4) C=sum^(-1/2) is a matrix obtained with Cholesky decomposition. Text say C^(T)C=sum^(-1) (see page 76 third paper) where "sum" indicates the variance-covariance matrix of returns.
5) ||x|| is (I quote from page 31 second link that I inserted) a general norm of a factor, depending on the modeler's preference, it can be L1,L2,L∞L1,L2,L∞ or DD-norm. Paper below
elaborates on the meaning of ||x|| but I don't understand well. At page 513, authors say to consider an uncertainty set for "\tilde{A}"with shape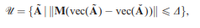 and Delta>=0, and for Proposition 1. of page 512 they say that we have to apply the definition of the Dual norm Lp, with M a diagonal matrix containing the inverses of the ranges of coefficient variation. This way to moodel the uncertainty results from the fact that "Let S be a closed, bounded convex set and consider an uncertainty set in which the uncertain coefficients are allowed to vary in such a way that the deviations from their nominal values fall in a convex set. [...] We consider uncertainty sets that arise from the requirement that the distance (as measured by an arbitrary norm) between uncertain coefficients and their nominal values is bounded."
and Delta>=0, and for Proposition 1. of page 512 they say that we have to apply the definition of the Dual norm Lp, with M a diagonal matrix containing the inverses of the ranges of coefficient variation. This way to moodel the uncertainty results from the fact that "Let S be a closed, bounded convex set and consider an uncertainty set in which the uncertain coefficients are allowed to vary in such a way that the deviations from their nominal values fall in a convex set. [...] We consider uncertainty sets that arise from the requirement that the distance (as measured by an arbitrary norm) between uncertain coefficients and their nominal values is bounded."
This is what I've understood, I hope you can help me to make clear my reasoning.
Since with a multiasset option we need to consider the correlation between asset prices included in the underlying basket of option, authors sugget (for independence and identically distribution, i.e. to say second order stationarity, that characterize log-returns, which implies the normality for CLT theorem: we are in a Black-Scholes environment) to study correlation between asset returns given the condition Rt=St/S0 that binds prices and returns. Clearly correlation should be evaluated between each m-th asset included in the basket (i.e. for each couple of asset on a set of M elements) and for each t-th instant of time. Obviously it's not the case to have such tremendous amount of information, moreover subject to uncertainty, so instead to constructing a random variance-covariance matrix for each t...
[i.e. to say considering, for each t, one by one, all the possible couples of assets and for any j-th possible realization of assets returns (for j=1,...,n and n the sample size) calculating the sum of cross products of deviations of these possibile realizations from their estimations]
...we use the properties of variance-covariance matrix (that I call "sum"). I know that sum is square, symmetric and positive definite, i.e. to say not-singular, i.e. to say invertible, so exists a sum^(-1). Since this matrix is also symmetric and positive definite I can factor it with Cholesky, that is an LU decomposition for symmetric and positive definite matrices. So, I should have an upper triangular matrix C with positive elements above the diagonal and a lower triangular normed matrix C^T (i.e. with all ones under under the diagonal). And because the intersection between t lower triangular matrices and t upper triangular matrices gives us t t diagonal matrices we should get M matrix.
But now I am confused.
A) How do we know that M contains the inverses of the ranges of coefficient variation? And what does it mean this proposition?
B) Authors say that modelling the uncertainty set of returns in that way ensure that, regardless of future realization of returns, the difference with their expectations will be always lower than a not-negative Delta. But why multiply M with the diff? What does it mean that product?
C) In the second paper (page 31), author gives us an example with the L1-norm:
Immagine-B
Does he only apply the definition of norm?
D) Authors say that the choice of a norm is discretional, but what does it involves choice a norm instead another one? What are the implications on the number of constraints of linear programming problem?
Thanks in advance for any help!
My first post concerns the evaluation of multiasset options in Robust Programming like you see from papers below
http://www.mit.edu/~dbertsim/papers/Robust Optimization/Robust Option Pricing.pdf
(page 848, 5.1)
https://dspace.mit.edu/bitstream/handle/1721.1/55108/591313102-MIT.pdf;sequence=2
(page 31, 6.1)
https://www.doc.ic.ac.uk/teaching/distinguished-projects/2012/n.rujeerapaiboon.pdf
(page 76, 6.2).
I write this post because I am trying to understand how the authors of these works arrive to the condition(page 848, 5.1)
https://dspace.mit.edu/bitstream/handle/1721.1/55108/591313102-MIT.pdf;sequence=2
(page 31, 6.1)
https://www.doc.ic.ac.uk/teaching/distinguished-projects/2012/n.rujeerapaiboon.pdf
(page 76, 6.2).
where
1) Gamma is a predefined parameter whose value reflects the degree of risk-tolerance of the investor, but for purposes of question it doesn't matter knowing what it means.
2)
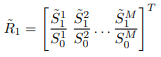 represents the vector of random returns for the first period (i.e. t=1) given the current price of m-th stock included in the underlying basket of multiasset option, for m=1,...,M.
represents the vector of random returns for the first period (i.e. t=1) given the current price of m-th stock included in the underlying basket of multiasset option, for m=1,...,M.3)
4) C=sum^(-1/2) is a matrix obtained with Cholesky decomposition. Text say C^(T)C=sum^(-1) (see page 76 third paper) where "sum" indicates the variance-covariance matrix of returns.
5) ||x|| is (I quote from page 31 second link that I inserted) a general norm of a factor, depending on the modeler's preference, it can be L1,L2,L∞L1,L2,L∞ or DD-norm. Paper below
elaborates on the meaning of ||x|| but I don't understand well. At page 513, authors say to consider an uncertainty set for "\tilde{A}"with shape
Fog...
This is what I've understood, I hope you can help me to make clear my reasoning.
Since with a multiasset option we need to consider the correlation between asset prices included in the underlying basket of option, authors sugget (for independence and identically distribution, i.e. to say second order stationarity, that characterize log-returns, which implies the normality for CLT theorem: we are in a Black-Scholes environment) to study correlation between asset returns given the condition Rt=St/S0 that binds prices and returns. Clearly correlation should be evaluated between each m-th asset included in the basket (i.e. for each couple of asset on a set of M elements) and for each t-th instant of time. Obviously it's not the case to have such tremendous amount of information, moreover subject to uncertainty, so instead to constructing a random variance-covariance matrix for each t...
[i.e. to say considering, for each t, one by one, all the possible couples of assets and for any j-th possible realization of assets returns (for j=1,...,n and n the sample size) calculating the sum of cross products of deviations of these possibile realizations from their estimations]
...we use the properties of variance-covariance matrix (that I call "sum"). I know that sum is square, symmetric and positive definite, i.e. to say not-singular, i.e. to say invertible, so exists a sum^(-1). Since this matrix is also symmetric and positive definite I can factor it with Cholesky, that is an LU decomposition for symmetric and positive definite matrices. So, I should have an upper triangular matrix C with positive elements above the diagonal and a lower triangular normed matrix C^T (i.e. with all ones under under the diagonal). And because the intersection between t lower triangular matrices and t upper triangular matrices gives us t t diagonal matrices we should get M matrix.
But now I am confused.
A) How do we know that M contains the inverses of the ranges of coefficient variation? And what does it mean this proposition?
B) Authors say that modelling the uncertainty set of returns in that way ensure that, regardless of future realization of returns, the difference with their expectations will be always lower than a not-negative Delta. But why multiply M with the diff? What does it mean that product?
C) In the second paper (page 31), author gives us an example with the L1-norm:
Immagine-B
Does he only apply the definition of norm?
D) Authors say that the choice of a norm is discretional, but what does it involves choice a norm instead another one? What are the implications on the number of constraints of linear programming problem?
Thanks in advance for any help!
