Boi
New member
- Joined
- Feb 14, 2023
- Messages
- 30
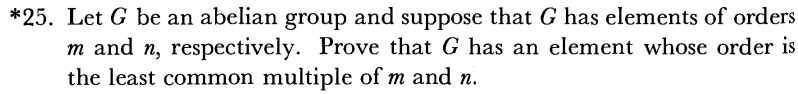
I'll be using [imath]o(g)[/imath] to denote the order of an element [imath]g[/imath].
For the proof I'll have to prove 2 lemmas first (they're very obvious results, but they are not stated in the book, so I've felt the need to prove them).
Lemma 1: If [imath]G[/imath] is a group, [imath]g \in G[/imath], [imath]o(g) = n[/imath], [imath]p, q \in \mathbb{Z}[/imath] and [imath]p \equiv q \; (\mathrm{mod} \; n)[/imath], then [imath]g^{p}=g^{q}[/imath].
