Proving theorem trouble

[Kostas]

NOTE: (read through question below first) I do not want to find the best distance that gives me the best angle possible (I already know this), I want to know why √(Z(Y+Z)) gives me the best distance that gives me the best angle possible.

The difficult question I was given in an assignment was where is the best distance possible to stand whilst viewing a painting to give the best viewing angle possible. I made a terrible diagram below for you to hopefully visualise this question better.




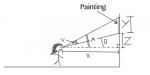
Pretty much this is a trigonometry problem and we are trying to find the best angle of view for a person standing Z meters below a painting that is Y meters in height and you are standing X meters away to view a painting. The painting is that little thicker line.
There is this equation to use where angle of view of the painting is
(tan^(-1)((Y+Z)/X)))-(tan^(-1) (Z/X))


We would be given a set Y and Z eg. the painting is 1 meter in height and is mounted 1 meter above eye level. To solve this problem we are supposed to use a zeroing in technique and continuously change the X value to get the best answer to one decimal place.


I'm lazy so I somehow came across this theory (I think that's what you call it.)
The theory is that √(Z(Y+Z)) = the best distance to stand to get the best viewing angle to view the painting. It works.
√(1(1+1)) = √2
standing √2 meters away will give you the best viewing angle of the painting.
I'v tried it with other painting heights and other heights mounted above eye level and it still works. The problem is that I don't know why this works and I'v tried to prove it but I can't. I have showed this to my teacher and my teacher doesn't understand either. Please help.


I have tried lot's of things to solve this. By using this theorem I tried finding other miscellaneous information about the triangle and I was trying to join the dots to see if it somehow proves the theory easier. I got nothing. I'm really struggling with this one please help me. You don't have to give the answer in great detail, you could lead me on the right direction to solving this answer like a hint would be greatly appreciated. Thanks.
I explain this better in my actual assignment that I wrote up here so if you don't quite understand this read the assignment.

 

[Deleted member 4993]

The difficult question I was given in an assignment was where is the best distance possible to stand whilst viewing a painting to give the best viewing angle possible. I made a terrible diagram below for you to hopefully visualise this question better.

View attachment 4226


Pretty much this is a trigonometry problem and we are trying to find the best angle of view for a person standing Z meters below a painting that is Y meters in height and you are standing X meters away to view a painting. The painting is that little thicker line.
There is this equation to use where angle of view of the painting is
(tan^(-1)((Y+Z)/X)))-(tan^(-1) (Z/X))


We would be given a set Y and Z eg. the painting is 1 meter in height and is mounted 1 meter above eye level. To solve this problem we are supposed to use a zeroing in technique and continuously change the X value to get the best answer to one decimal place.


I'm lazy so I somehow came across this theory (I think that's what you call it.)
The theory is that √(Z(Y+Z)) = the best distance to stand to get the best viewing angle to view the painting. It works.
√(1(1+1)) = √2
standing √2 meters away will give you the best viewing angle of the painting.
I'v tried it with other painting heights and other heights mounted above eye level and it still works. The problem is that I don't know why this works and I'v tried to prove it but I can't. I have showed this to my teacher and my teacher doesn't understand either. Please help.


I have tried lot's of things to solve this. By using this theorem I tried finding other miscellaneous information about the triangle and I was trying to join the dots to see if it somehow proves the theory easier. I got nothing. I'm really struggling with this one please help me. You don't have to give the answer in great detail, you could lead me on the right direction to solving this answer like a hint would be greatly appreciated. Thanks.

What is the definition of best viewing angle?

 

[HallsofIvy]

Basically, you have two right triangles.

The line from your eye to the bottom of the picture, the wall, and the line from your eye perpendicular to the wall is a right triangle with "opposite side" of length Z and "near side" of length X. Taking the angle at your eye to be \(\displaystyle \theta\) we have \(\displaystyle tan(\theta)= \frac{Z}{X}\).

The line from your eye to the top of the picture, the wall, and the line from your eye to the perpendicular to the wal is a right triangle with "opposite side" of length Z+ Y and "near side" X. Taking the angle at your eye to be \(\displaystyle \phi\) we have \(\displaystyle tan(\phi)= \frac{Z+ Y}{X}\).

To "best viewing position" will be the value of X that maximizes the angle the picture itself subtends, \(\displaystyle \phi- \theta\).

Now use a trig identity to write \(\displaystyle tan(\phi- \theta)\) in terms of \(\displaystyle tan(\phi)\) and \(\displaystyle tan(\theta)\) and so in terms of X.

 

[Kostas]

To subhotosh khan, The best viewing angle is V in the diagram, the best viewing angle is the biggest angle V, as you move closer and further away from the painting (change X) V changes and we want V to be the biggest. V is also angle A - angle B. (tan^(-1)((Y+Z)/X)))-(tan^(-1) (Z/X)) Sorry, I have a habit of not explaining things properly. It might still not make sense lol. Is there anything else I was unclear about?

 

[Deleted member 4993]

using wolframalpha:

best viewing angle (under the given physical constraints) at:

X = √(Y)*√(Y+Z)