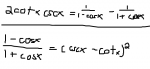thebeanstalk
New member
- Joined
- Aug 16, 2016
- Messages
- 7
Hello,
I was stuck proving these given identities
*2cotx cscx - 1/1-cosx - 1/1+cosx "2cotx * cscx equals 1 over 1-cosx minus 1 over 1+cosx"
What I did here is:
I multiplty both sides by (1-cosx)(1+cosx) to get the denominator 1/1-cosx - 1/1+cosx so the answer is (1-cosx) + (1+cosx) all over (1-cosx)(1+cosx) and after that I was stuck
*1-cosx/1+cosx = (cscx - cotx)^2 "1-cosx over 1+cosx is equal to quantity cscx - cotx squared"
Hope this will get an answer. Thank you very much!
I was stuck proving these given identities
*2cotx cscx - 1/1-cosx - 1/1+cosx "2cotx * cscx equals 1 over 1-cosx minus 1 over 1+cosx"
What I did here is:
I multiplty both sides by (1-cosx)(1+cosx) to get the denominator 1/1-cosx - 1/1+cosx so the answer is (1-cosx) + (1+cosx) all over (1-cosx)(1+cosx) and after that I was stuck
*1-cosx/1+cosx = (cscx - cotx)^2 "1-cosx over 1+cosx is equal to quantity cscx - cotx squared"
Hope this will get an answer. Thank you very much!
Attachments
Last edited: