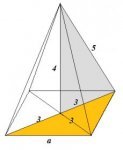
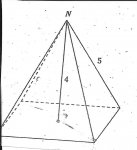
In the figure below, the pyramid has a height of 4. Each of the four edges that meet a N has a length of 5. What is the area of the square base?
 If you need a closer picture, I can email you one.
If you need a closer picture, I can email you one.
I have the explanation for the problem, but I don't understand the thought process of the author. The height and the edge make it apparent that it is a 3-4-5 triangle, and the base is 6. The explanation says "The height and edge of the pyramid form a 3-4-5 right triangle with line AB in the figure (an additional line is drawn diagonally). Thus AB=3, so BC=6. So the side of the base is 6/the square root of 2. Use this in the formula for the area of a square" I don't get how the author got 6/square root of 2. . If anyone could explain how 6/square root of 2 was gotten, that would be great.
 If you need a closer picture, I can email you one.
If you need a closer picture, I can email you one.I have the explanation for the problem, but I don't understand the thought process of the author. The height and the edge make it apparent that it is a 3-4-5 triangle, and the base is 6. The explanation says "The height and edge of the pyramid form a 3-4-5 right triangle with line AB in the figure (an additional line is drawn diagonally). Thus AB=3, so BC=6. So the side of the base is 6/the square root of 2. Use this in the formula for the area of a square" I don't get how the author got 6/square root of 2. . If anyone could explain how 6/square root of 2 was gotten, that would be great.
Attachments
Last edited: