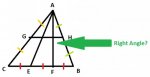
Given:
Triangle ABC,
Lines AE, AF trisect side BC, with AE to the left of AF, and points E, F on line BC,
Points G, H bisect sides AC, AB respectively.
Are the angles formed by lines AF and GH right angles?
I am stuck on this problem, and so far I proved triangle AHG similar to ABC by a ratio of 1:2, since G, H bisect AB and AC (side splitter theorem).
Triangle ABC,
Lines AE, AF trisect side BC, with AE to the left of AF, and points E, F on line BC,
Points G, H bisect sides AC, AB respectively.
Are the angles formed by lines AF and GH right angles?
I am stuck on this problem, and so far I proved triangle AHG similar to ABC by a ratio of 1:2, since G, H bisect AB and AC (side splitter theorem).