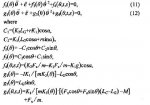Hi everyone,
I have two second order differential equations with boundary conditions (11) & (12) as shown in the attached figure. The author has generated a graph between Ɵ and t as a result of solving these equations. I need clarifications on how the author got the graph with the two differential equations. Thanks in advance
\(\displaystyle f_1(\theta)\ddot{\theta}\, +\, \ddot{\epsilon}\, +\, f_3(\theta)\dot{\theta}^2\, +\, f_4(\theta,\, t,\, \epsilon)\, =\, 0,\qquad(11)\)
\(\displaystyle g_1(\theta)\ddot{\theta}\, +\, \ddot{\epsilon}\, +\, g_3(\theta)\dot{\theta}^2\, +\, g_4(\theta,\, t,\, \epsilon)\, =\, 0,\qquad(12)\)
\(\displaystyle \mbox{where}\)
\(\displaystyle C_1\, =\, (K_2 L_G\, +\, rK_1)\cos(\alpha),\)
\(\displaystyle C_2\, =\, K_1(L_G \cos(\alpha)\, +\, r\sin(\alpha)),\)
\(\displaystyle f_1(\theta)\, =\, -C_1 \cos(\theta)\, +\, C_2 \sin(\theta),\)
\(\displaystyle f_3(\theta)\, =\, C_2 \cos(\theta)\, +\, C_1 \sin(\theta),\)
\(\displaystyle f_4(\theta,\, \epsilon,\, t)\, =\, \left(K_2 F_x / m\, -\, K_1 F_z / m\, -\, K_1 g\right) \cos(\alpha),\)
\(\displaystyle g_1(\theta)\, =\, -IK / \left[mK_3(\theta)\right]\, -\, L_G \cos(\theta),\)
\(\displaystyle g_3(\theta)\, =\, L_G \sin(\theta),\)
\(\displaystyle g_4(\theta,\, \epsilon,\, t)\, =\, K_1 / \left[mK_3(\theta)\right]\, \cdot\, \left[(F_x \cos(\theta)\, +\, F_z \sin(\theta))(L_C\, -\, L_G)\, -\, M\right]\, +\, F_x / m\)
Note: Ɵ, £, t are the variables, Lg ,α and all others are constant and known values.
I have two second order differential equations with boundary conditions (11) & (12) as shown in the attached figure. The author has generated a graph between Ɵ and t as a result of solving these equations. I need clarifications on how the author got the graph with the two differential equations. Thanks in advance
\(\displaystyle f_1(\theta)\ddot{\theta}\, +\, \ddot{\epsilon}\, +\, f_3(\theta)\dot{\theta}^2\, +\, f_4(\theta,\, t,\, \epsilon)\, =\, 0,\qquad(11)\)
\(\displaystyle g_1(\theta)\ddot{\theta}\, +\, \ddot{\epsilon}\, +\, g_3(\theta)\dot{\theta}^2\, +\, g_4(\theta,\, t,\, \epsilon)\, =\, 0,\qquad(12)\)
\(\displaystyle \mbox{where}\)
\(\displaystyle C_1\, =\, (K_2 L_G\, +\, rK_1)\cos(\alpha),\)
\(\displaystyle C_2\, =\, K_1(L_G \cos(\alpha)\, +\, r\sin(\alpha)),\)
\(\displaystyle f_1(\theta)\, =\, -C_1 \cos(\theta)\, +\, C_2 \sin(\theta),\)
\(\displaystyle f_3(\theta)\, =\, C_2 \cos(\theta)\, +\, C_1 \sin(\theta),\)
\(\displaystyle f_4(\theta,\, \epsilon,\, t)\, =\, \left(K_2 F_x / m\, -\, K_1 F_z / m\, -\, K_1 g\right) \cos(\alpha),\)
\(\displaystyle g_1(\theta)\, =\, -IK / \left[mK_3(\theta)\right]\, -\, L_G \cos(\theta),\)
\(\displaystyle g_3(\theta)\, =\, L_G \sin(\theta),\)
\(\displaystyle g_4(\theta,\, \epsilon,\, t)\, =\, K_1 / \left[mK_3(\theta)\right]\, \cdot\, \left[(F_x \cos(\theta)\, +\, F_z \sin(\theta))(L_C\, -\, L_G)\, -\, M\right]\, +\, F_x / m\)
Note: Ɵ, £, t are the variables, Lg ,α and all others are constant and known values.
Attachments
Last edited by a moderator: