A friend of mine stumped me with this math problem, I can't seem to think I'm forgetting something...
After about an hour I think I solved it but I'm not sure so I'm going to need some help! Thank you.
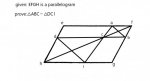
Edit:fixed
I believe that you have to prove DE and AB parallel and then use the vertical angles from DCE and CAB as well as an alternate exterior angle to prove them similar by AA~. I'm just not too sure on how to prove DI || AB.
Edit 2: Just figured it out. Instead of finding any lines parallel I used proportions after AA~ and then used SAS to prove ABC ~ DCE.
After about an hour I think I solved it but I'm not sure so I'm going to need some help! Thank you.

Edit:fixed
I believe that you have to prove DE and AB parallel and then use the vertical angles from DCE and CAB as well as an alternate exterior angle to prove them similar by AA~. I'm just not too sure on how to prove DI || AB.
Edit 2: Just figured it out. Instead of finding any lines parallel I used proportions after AA~ and then used SAS to prove ABC ~ DCE.
Last edited:
