patbuzzatto
New member
- Joined
- Jul 1, 2017
- Messages
- 1
Hi, I have the exercise in the image that I need to resolve by method of variation of parameters:
7.1 A particle of unit mass moves in a straight line according to the following differential equation:
. . .\(\displaystyle \dfrac{d^2 x}{dt^2}\, =\, g(1\, +\, \epsilon x)\)
...where g and \(\displaystyle \epsilon\) are constants and \(\displaystyle 0\, <\, \epsilon x\, \ll\, 1.\) Use the method of the variation of parameters to show that the particle's motion is given approximately by:
. . .\(\displaystyle x\, =\, at\, +\, b\, +\, \frac{1}{2}gt^2\big[1\, +\, \epsilon \left(\frac{1}{12}gt^2\, +\, \frac{1}{3}at\, +\, b\right)\big]\)
...where a and b are the values of \(\displaystyle \frac{dx}{dt}\) and x at t = 0.
unfortunately I can't understand how it works for this equation, could someone help me?
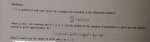
7.1 A particle of unit mass moves in a straight line according to the following differential equation:
. . .\(\displaystyle \dfrac{d^2 x}{dt^2}\, =\, g(1\, +\, \epsilon x)\)
...where g and \(\displaystyle \epsilon\) are constants and \(\displaystyle 0\, <\, \epsilon x\, \ll\, 1.\) Use the method of the variation of parameters to show that the particle's motion is given approximately by:
. . .\(\displaystyle x\, =\, at\, +\, b\, +\, \frac{1}{2}gt^2\big[1\, +\, \epsilon \left(\frac{1}{12}gt^2\, +\, \frac{1}{3}at\, +\, b\right)\big]\)
...where a and b are the values of \(\displaystyle \frac{dx}{dt}\) and x at t = 0.
unfortunately I can't understand how it works for this equation, could someone help me?
Last edited by a moderator:
