Thank you for your reply. I think we’re converging on the core of our disagreement: how we treat assumptions versus facts, and how they function in a proof.
That’s actually the point I was trying to make. If you assume something (like Paris is the U.S. capital), you're not saying it’s a fact—you’re creating a hypothetical scenario. The truth or falsity of that assumption doesn’t matter at first; we analyze its consequences. If assuming Paris is the capital leads to a contradiction (e.g., Washington, D.C. is already the capital), then the assumption must be false.
That’s exactly how proof by contradiction works:
Here is one:
Book: Inledande geometri för högskolestudier by Stefan Diehl,
Theorem 21 (page 43): A tangent to a circle is perpendicular to the radius at the point of contact.
Theorem 21.
A tangent to a circle is perpendicular to the radius at the point of tangency.
Proof (by contradiction):
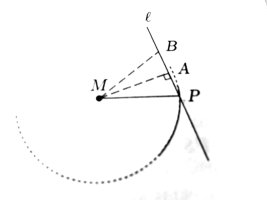
Assume there exists a tangent line [imath]l[/imath] that is not perpendicular to the radius drawn from the center [imath]M[/imath] to the point of tangency [imath]P[/imath].
Draw the perpendicular (the normal) from [imath]M[/imath] to [imath]l[/imath]; let this line intersect [imath]l[/imath] at a point [imath]A[/imath], where [imath]A \ne P[/imath].
Now, mark a point [imath]B \ne P[/imath] on [imath]l[/imath] such that [imath]PA = AB[/imath], and draw the segment [imath]MB[/imath].
We now consider triangles [imath]\triangle AMP[/imath] and [imath]\triangle AMB[/imath]:
[imath]\triangle AMP \cong \triangle AMB[/imath].
Hence, [imath]MP = MB[/imath], so [imath]B[/imath] also lies on the circle (since its distance to the center is equal to the radius).
But this contradicts the assumption that [imath]l[/imath] is a tangent, since a tangent intersects a circle in exactly one point.
[imath]\Rightarrow[/imath] Contradiction. Therefore, our initial assumption was false.
Thus, the tangent [imath]l[/imath] must be perpendicular to the radius at point [imath]P[/imath].
If I assume that Paris is the capital of the United States, are you sure that my assumption is a fact? If that is a fact, then I am confused!'
That’s actually the point I was trying to make. If you assume something (like Paris is the U.S. capital), you're not saying it’s a fact—you’re creating a hypothetical scenario. The truth or falsity of that assumption doesn’t matter at first; we analyze its consequences. If assuming Paris is the capital leads to a contradiction (e.g., Washington, D.C. is already the capital), then the assumption must be false.
That’s exactly how proof by contradiction works:
- Assume something (e.g., a line is tangent to a circle),
- Follow its logical consequences,
- If it leads to a contradiction, then the assumption is false.
Thank you for your challenge. You asked for a reference (non-Russian) where the theorem is proved by contradiction, assuming that a line is tangent to a circle.Give me the name of one book (or one author) that proves this Theorem by contradiction and says we assume \(\displaystyle m\) is tangent to the circle! You have the freedom to exclude the Russian authors.
Here is one:
Book: Inledande geometri för högskolestudier by Stefan Diehl,
Theorem 21 (page 43): A tangent to a circle is perpendicular to the radius at the point of contact.
Theorem 21.
A tangent to a circle is perpendicular to the radius at the point of tangency.
Proof (by contradiction):
Assume there exists a tangent line [imath]l[/imath] that is not perpendicular to the radius drawn from the center [imath]M[/imath] to the point of tangency [imath]P[/imath].
Draw the perpendicular (the normal) from [imath]M[/imath] to [imath]l[/imath]; let this line intersect [imath]l[/imath] at a point [imath]A[/imath], where [imath]A \ne P[/imath].
Now, mark a point [imath]B \ne P[/imath] on [imath]l[/imath] such that [imath]PA = AB[/imath], and draw the segment [imath]MB[/imath].
We now consider triangles [imath]\triangle AMP[/imath] and [imath]\triangle AMB[/imath]:
- [imath]PA = AB[/imath] (by construction),
- [imath]\angle PAM = \angle BAM = 90^\circ[/imath] (since [imath]AM[/imath] is the normal to [imath]l[/imath]),
- [imath]AM[/imath] is a common side.
[imath]\triangle AMP \cong \triangle AMB[/imath].
Hence, [imath]MP = MB[/imath], so [imath]B[/imath] also lies on the circle (since its distance to the center is equal to the radius).
But this contradicts the assumption that [imath]l[/imath] is a tangent, since a tangent intersects a circle in exactly one point.
[imath]\Rightarrow[/imath] Contradiction. Therefore, our initial assumption was false.
Thus, the tangent [imath]l[/imath] must be perpendicular to the radius at point [imath]P[/imath].
Last edited: