logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,253
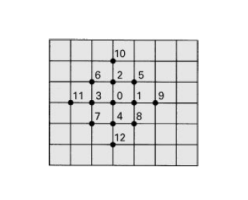
Referring to the figure, demonstrate that the biharmonic equation
\(\displaystyle \nabla^4w = \frac{\partial^4 w}{\partial x^4} + 2\frac{\partial^4 w}{\partial x^2 \partial y^2} + \frac{\partial^4 w}{\partial y^4} = 0\)
takes the following finite difference form:
\(\displaystyle h^4\nabla^4w = 20w_0 - 8(w_1 + w_2 + w_3 + w_4) + 2(w_5 + w_6 + w_7 + w_8) + w_9 + w_{10} + w_{11} + w_{12}\)
\(\displaystyle \nabla^4w = \frac{\partial^4 w}{\partial x^4} + 2\frac{\partial^4 w}{\partial x^2 \partial y^2} + \frac{\partial^4 w}{\partial y^4} = 0\)
takes the following finite difference form:
\(\displaystyle h^4\nabla^4w = 20w_0 - 8(w_1 + w_2 + w_3 + w_4) + 2(w_5 + w_6 + w_7 + w_8) + w_9 + w_{10} + w_{11} + w_{12}\)

