Trigonometry Help: Surveyor needs to determine height of building. She measures...

[njbeep]

[FONT=Helvetica Neue, Helvetica, Arial, sans-serif]Hi there,[/FONT]

[FONT=Helvetica Neue, Helvetica, Arial, sans-serif]I am attempting to answer (b) below, but i am not quite sure how to calculate the resulting equation.

[/FONT]The question:
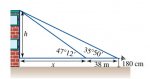
[FONT=Helvetica Neue, Helvetica, Arial, sans-serif]A surveyor needs to determine the height of a building. She measures the angle of elevation of the top of the building from two points, 38 m apart. The surveyor’s eye level is 180 cm above the ground. [/FONT]
[FONT=&quot]a Find two expressions for the height of the building, h, in terms of x using the two angles. (DONE) [/FONT]
[FONT=&quot]b Solve for x by equating the two expressions obtained in a. [/FONT]
[FONT=&quot]c Find the height of the building. [/FONT]

[FONT=Helvetica Neue, Helvetica, Arial, sans-serif]Attached below is the picture in the workbook. I am just struggling how to solve for x. This is what i have so far:

[/FONT][FONT=&quot]The answer to a is:
[/FONT][FONT=Helvetica Neue, Helvetica, Arial, sans-serif]h= xtan(47[/FONT]°[FONT=Helvetica Neue, Helvetica, Arial, sans-serif]12')m[/FONT]
[FONT=Helvetica Neue, Helvetica, Arial, sans-serif]h=(x+38)tan(32[/FONT]°[FONT=Helvetica Neue, Helvetica, Arial, sans-serif]51')m[/FONT]

[FONT=Helvetica Neue, Helvetica, Arial, sans-serif]I checked with classmates, and it is correct.[/FONT]

For b, so far i have this:

Since [FONT=&quot](h) equals itself,

xtan(47º12') = (x + 38) tan(32º51')
[/FONT][FONT=&quot]xtan(47º12') - xtan(32º51') = 38tan(32º51')

[/FONT]I don't even know if this much is correct or if i am on the right track. Not much clue where to go from here so any will be greatly appreciated!
Thank you in advance.

 

[stapel]

A surveyor needs to determine the height of a building. She measures the angle of elevation of the top of the building from two points, 38 m apart. The surveyor’s eye level is 180 cm above the ground.
a Find two expressions for the height of the building, h, in terms of x using the two angles. (DONE)
b Solve for x by equating the two expressions obtained in a.
c Find the height of the building.

Attached below is the picture in the workbook.

I am just struggling how to solve for x. This is what i have so far:

The answer to a is:
h= xtan(47°12')m
h=(x+38)tan(32°51')m

I checked with classmates, and it is correct.

You don't show your work. I will assume that you did something along the lines of the following:

. . . . .\(\displaystyle \tan(47^{\circ} \, 12')\, =\, \dfrac{h}{x}\, \Rightarrow\, x\, \tan(47^{\circ} \, 12')\, =\, h\)

. . . . .\(\displaystyle \tan(35^{\circ}\, 50')\, =\, \dfrac{h}{x\, +\, 38}\, \Rightarrow\, (x\, +\, 38)\, \tan(35^{\circ}\, 50')\, =\, h\)

Then you set the two "h=" expressions equal to each other, to create your equation:

For b, so far i have this:

Since (h) equals itself,

xtan(47º12') = (x + 38) tan(32º51')
xtan(47º12') - xtan(32º51') = 38tan(32º51')

Now take the common factor on the left-hand side (that is, the x) out front, and divide through by what's left.

 

[stapel]

You don't show your work. I will assume that you did something along the lines of the following:

. . . . .\(\displaystyle \tan(47^{\circ} \, 12')\, =\, \dfrac{h}{x}\, \Rightarrow\, x\, \tan(47^{\circ} \, 12')\, =\, h\)

. . . . .\(\displaystyle \tan(35^{\circ}\, 50')\, =\, \dfrac{h}{x\, +\, 38}\, \Rightarrow\, (x\, +\, 38)\, \tan(35^{\circ}\, 50')\, =\, h\)

Then you set the two "h=" expressions equal to each other, to create your equation...

I completely overlooked the "180 cm", which is 1.8 m, in the diagram. (It may represent something like the height, above ground, of the measuring instrument being used.) Have you remembered to add that portion of the height to "h", to get the overall height?

 

[njbeep]

I completely overlooked the "180 cm", which is 1.8 m, in the diagram. (It may represent something like the height, above ground, of the measuring instrument being used.) Have you remembered to add that portion of the height to "h", to get the overall height?

Thank you for your explanations so far. I am still struggling to understand how, from x, we get the answer.

The book says the answer to b) 76.69 m and to c) 84.62 m

My working out is as follows:


xtan(47º12') - xtan(32º51') = 38tan(32º51')

Taking out the common factor as you suggested, we get:

x[tan(47º12') - tan(32º51')] = 38tan(32º51')

Therefore:

x = [38tan(32º51')] / [tan(47º12') - tan(32º51')]

When calculated:

x = 24.5363 / 0.43421 = 56.50791

I then add that to 38 m so i can get the total length of the adjacent:

Length of the Adjacent = 56.50791 + 38 = 94.51 m

Now i can use this and the tan function to calculate the height (h, or the opposite):

tanθ = Opposite / Adjacent
tan35º50' = h (opposite side) / 94.51
h = 68.25 m

But even if i add the 1.8 m (180 cm in the diagram), i still don't come close to answer in the back of the book.

What steps am i missing here?
Thanks so much for your time.

 

[njbeep]

38tan(32º51') : where does that angle come from?
Not show n in diagram.

And what is the purpose of "180 cm" shown in diagram?

Let u = shorter hypotenuse, v = other hypotenuse
Then:
x = (v^2 - u^2 - 1444) / 76
Do you follow that?

Oh, i've made a typo error! Yes i follow that now.

I'm sorry to have wasted your time, but i truly appreciate it.

Thank you.

 

[njbeep]

I completely overlooked the "180 cm", which is 1.8 m, in the diagram. (It may represent something like the height, above ground, of the measuring instrument being used.) Have you remembered to add that portion of the height to "h", to get the overall height?

I've made a typo error. I'm very sorry to have wasted your time, it all makes sense now.

Thank you again for pointing out i had to factorise the expression and then divide it out to get x alone.
Lesson learnt!