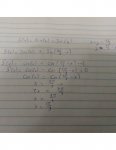Hi, everybody
I have this problem :
(3) When \(\displaystyle x\, +\, y\, =\, \dfrac{2\pi}{3},\, x\, \geq\, 0,\, y\, \geq\, 0,\) the maximum of \(\displaystyle \sin(x)\, +\, \sin(y)\)
is \(\displaystyle \boxed{(1)\qquad\\ \qquad}\) and the minimum of that expression is \(\displaystyle \boxed{(2)\qquad\\ \qquad}\)
I found the maximum(√3) an minimum(√3/2) values using logic and a sketch of the trigonometric circle.
I want to know a way to find the answer using more math instead of the way I did, because maybe it was only luck to find it. Or even better a clue to see if I could find it. Thanks
I have this problem :
(3) When \(\displaystyle x\, +\, y\, =\, \dfrac{2\pi}{3},\, x\, \geq\, 0,\, y\, \geq\, 0,\) the maximum of \(\displaystyle \sin(x)\, +\, \sin(y)\)
is \(\displaystyle \boxed{(1)\qquad\\ \qquad}\) and the minimum of that expression is \(\displaystyle \boxed{(2)\qquad\\ \qquad}\)
I found the maximum(√3) an minimum(√3/2) values using logic and a sketch of the trigonometric circle.
I want to know a way to find the answer using more math instead of the way I did, because maybe it was only luck to find it. Or even better a clue to see if I could find it. Thanks
Attachments
Last edited by a moderator: