Hi! I was going through a question from my textbook and I think I'm missing some conceptual understanding of the topic because I'm having a hard time grasping the provided solution.
Question:
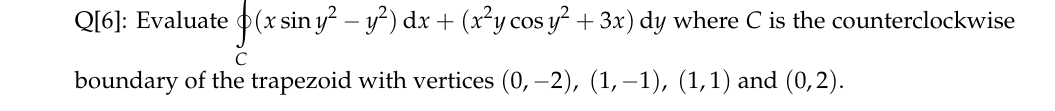
Solution:
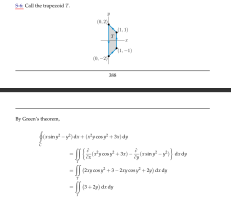

I understand the simplification after applying Green's Theorem, but I'd like to double check if I'm understanding their reasoning for getting rid of the double integral of 2y correctly. The way I imagine it starts by assuming that 3+2y is a function in the z-axis (since we're integrating with respect to x and y), giving:
[math]z = 3 +2y[/math]
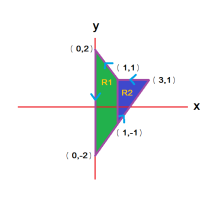
Then, since we're splitting the intergal and only looking at 2y, we ignore the 3 for now. The integration domain (i.e. the trapezoid) is symmetric across the x-axis, and since we're calculating the volume from [imath]z=2y[/imath] to the xy-plane with [imath]z = |2y|[/imath] being symmetric across the zx-plane, the first integral will be 0, meaning the second one will also yield 0. In other words, the volumes under [imath]z = 2y[/imath] on either side of the z-axis will be equal in magnitude but opposite in sign, so they cancel out. Is that correct? If so, how would I go about recognizing this type of pattern in the future? I only realized this after seeing the solution and drawing out the surfaces, and this time the equations were quite nice. However, assuming this doesn't always work since not all equations will be symmetric in this way, is this type of analysis simply a habit I should just get used to, even with harder equations?
Thank you so much in advance!
Question:
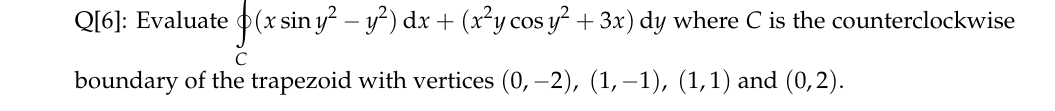
Solution:


I understand the simplification after applying Green's Theorem, but I'd like to double check if I'm understanding their reasoning for getting rid of the double integral of 2y correctly. The way I imagine it starts by assuming that 3+2y is a function in the z-axis (since we're integrating with respect to x and y), giving:
[math]z = 3 +2y[/math]
Then, since we're splitting the intergal and only looking at 2y, we ignore the 3 for now. The integration domain (i.e. the trapezoid) is symmetric across the x-axis, and since we're calculating the volume from [imath]z=2y[/imath] to the xy-plane with [imath]z = |2y|[/imath] being symmetric across the zx-plane, the first integral will be 0, meaning the second one will also yield 0. In other words, the volumes under [imath]z = 2y[/imath] on either side of the z-axis will be equal in magnitude but opposite in sign, so they cancel out. Is that correct? If so, how would I go about recognizing this type of pattern in the future? I only realized this after seeing the solution and drawing out the surfaces, and this time the equations were quite nice. However, assuming this doesn't always work since not all equations will be symmetric in this way, is this type of analysis simply a habit I should just get used to, even with harder equations?
Thank you so much in advance!