Well, it LOOKED deceptively simple...

[HaoDaMao]

Isn't that how questions always start? So I'm a bit stumped, and wondering if someone here has an idea. I'm usually pretty good with geometry, but this one, for some reason, has be a bit stuck! Here's the problem:

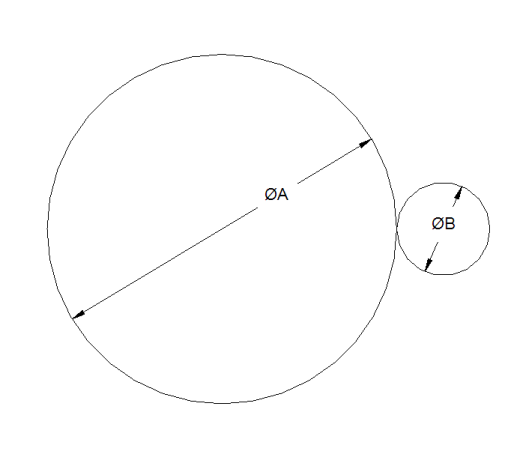
Given a large circle of diameter A, how many smaller circles of diameter B will fit around it, such that none overlap? Yeah, it's tricky! I started with the "go to the diameter, and find the spacing", but as circles pack tighter you end up with circles touching at points on a chord, rather than the diameter. And that doesn't always work!

So any ideas on this brain teaser?

 

[Deleted member 4993]

Draw tangents to the smaller circle - from the center of the larger circle. These will be common tangets to the touching smaller circles.

The sum of the angles between all the tangents would be ? 2?.

 

[HaoDaMao]

But would the tangents be to the diameter of smaller circle, or a smaller chord?

 

[Denis]

EXAMPLE: Get some paper and draw a circle radius 3, and a circle radius 2 tangent to it:
distance from the 2 centers = 5, right?

From center of larger circle, draw 2 tangent lines to smaller circle:
you get 2 right triangles, hypotenuse = 5, short leg = 2, right?

Now calculate angle created by the 2 tangent lines. OK?

 

[HaoDaMao]

Yes, but here's the rub - how do you determine where to set those tangent lines? It's not to the diameter - that creates overlap. The key is to determine the point of tangent on circle B...

 

[Denis]

Yes, but here's the rub - how do you determine where to set those tangent lines? It's not to the diameter - that creates overlap. The key is to determine the point of tangent on circle B...

We need to determine the angle created by the tangent lines; let that angle = Q:
Q = 2 * ARCSIN(k) where k = [B / (A + B)]
Then the number of possible smaller circles = FLOOR(360 / Q).

Using example I used previously: A = 3, B = 2:
Q = ~47.156...
FLOOR(360 / 47.156...) = 7